Lokale Extrema

Eine Funktion f:D⊂Rn→Rf:D\subset \R^n\rightarrow\R besitzt in x∈Dx\in D ein lokales Maximum (bzw. lokales Minimum), falls eine Umgebung Uε(x)⊂DU_\varepsilon (x)\subset D existiert, so dass f(x)≥f(y)f(x)\geq f(y) (bzw. f(x)≤f(y)f(x)\leq f(y)) für alle y∈Uε(x)y\in U_\varepsilon(x). Tritt in dieser Definition der Fall f(x)=f(y)f(x)=f(y) nur für x=yx=y ein, so spricht man von einem isolierten lokalen Maximum bzw. Minimum. Ein lokales Extremum ist ein lokales Maximum oder lokales Minimum.
Es wird nur etwas über das Verhalten von ff in Uε(x)U_\varepsilon(x) ausgesagt. Die Funktion kann noch weitere (lokale) Extrema besitzen, insbesondere auch globale, also Extremwerte von ff auf dem ganzen Definitionsbereich DD.
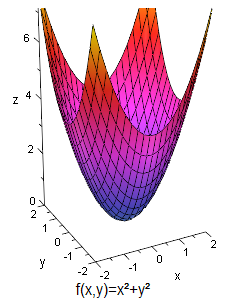
x2y2.png

Beispiel

Die Funktion f (x1,x2)=x12+x22f\, (x_1,x_2)=x_1^2+x_2^2 besitzt in jeder Umgebung um den Ursprung in (0,0)(0,0) das relative Minimum f(0,0)=0f(0,0)=0. Es ist zugleich globales Minimum auf D(f)=R2D(f)=\R^2.

Satz 16KP (notwendige Bedingung für lokale Extrema)

Sei D⊂RnD\subset \R^n offen und f:D→Rf:D\rightarrow\R eine partiell differenzierbare Funktion. Dann gilt: wenn ff in x∈Dx\in D ein lokales Extremum besitzt, dann verschwindet der Gradient von ff an der Stelle xx, also grad⁡f(x)=0\grad f(x)=0. Dies ist gleichbedeutend mit dem Verschwinden aller partiellen Ableitungen ∂f∂x1(x)=⋯=∂f∂x1(x)=0\dfrac{\partial f}{\partial x_1}(x)=\dots= \dfrac{\partial f}{\partial x_1}(x)=0

Beweis

Wir definieren φi(t):=f(x+tei)\varphi_i(t):=f(x+te_i) für i=1,…,n i=1,\dots,n und sei ei=(0⋮1⋮0) e_i=\begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix} der ii-te Einheitsvektor. Da ff in xx ein lokales Extremum besitzt, hat nach Definition die φi\varphi_i in t=0t=0 ein lokales Extremum. Somit gilt nach Satz 15VG φi′(0)=0=lim⁡t→0f(x+tei)−f(x)t=∂f∂xi(x)\varphi_i'(0)=0=\lim_{t\rightarrow 0} \dfrac{f(x+te_i)- f(x)}{t}=\dfrac{\partial f}{\partial x_i}(x). Also gilt für den Gradienten grad⁡f(x)=(∂f∂xi(x),…,∂f∂xn(x))=0\grad f(x)=\left(\dfrac{\partial f}{\partial x_i}(x),\dots, \dfrac{\partial f}{\partial x_n}(x)\right)=0. □\qed

Beispiele

Für die Funktion f(x1,x2)=x12+x22f(x_1,x_2)=x_1^2+x_2^2 mit dem Minimum im Ursprung in (0,0)(0,0) gilt: ∂f∂x1=2x1\dfrac{\partial f}{\partial x_1} =2x_1 und ∂f∂x2=2x2\dfrac{\partial f}{\partial x_2} =2x_2. Beide partiellen Ableitungen verschwinden im Ursprung.
Das obige Kriterium ist für die Existenz eines relativen Extremwertes nicht hinreichend, wie das folgende Beispiel zeigt.
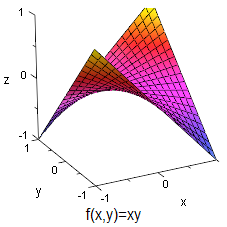
xy.png
Für f(x1,x2)=x1⋅x2f(x_1,x_2)=x_1\cdot x_2 gilt: ∂f∂x1=x2\dfrac{\partial f}{\partial x_1} =x_2 und ∂f∂x2=x1\dfrac{\partial f}{\partial x_2} =x_1. Für a=(0,0)a=(0,0) ist damit fx1(a)=fx2(a)=0f_{x_1}(a)=f_{x_2}(a)=0. Die Funktion nimmt dort aber kein Minimum an, da f(−1,1)=−1<0f(-1,1)=-1<0 gilt. Bei (0,0)(0,0) handelt es sich um einen so genannten Sattelpunkt.
 
 

An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mehrdimensionale Analysis