Funktionen mehrerer Veränderlicher

Die Definition reeller Funktionen kann auf mehrere Veränderliche erweitert werden. Bei nn Veränderlichen ist der Definitionsbereich DD eine Teilmenge des Rn\Rn. Durch eine Funktion ff wird dabei einem n-Tupel des Rn\Rn eine reelle Zahl zugeordnet. Man schreibt:
f:Rn⊇D→Rf:\Rn\supseteq D\to \R
Die Punktemenge DD heißt der Definitionsbereich der Funktion ff und wird mit D(f)D(f) bezeichnet. Alle y∈Ry\in\R, die als Funktionswerte auftreten bilden den Wertebereich der Funktion ff und dieser wird mit W(f)W(f) bezeichnet.
Wenn x=(x1,x2,…,xn)x=(x_1,x_2,\dots,x_n) schreibt man für den Funktionswert
y:=f(x)=f(x1,x2,…,xn)y:=f(x)=f(x_1,x_2,\dots,x_n).(1)
Eine Funktion braucht nicht explizit wie in (1) gegeben zu sein sondern kann auch implizit durch eine Gleichung der Form F(x1,x2,…,xn,y)=0F(x_1,x_2,\dots,x_n,y)=0 definiert werden.

Beispiel 165O

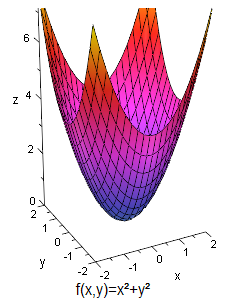
x2y2.png
Sei f:R2→Rf:\domRZwei\to\R durch folgende Gleichung gegeben
f(x1,x2)=x12+x22f(x_1,x_2)=x_1^2+x_2^2
Der Definitionsbereich von ff ist der gesammte R2\domRZwei, also D(f)=R2D(f)=\domRZwei. Als Werte können nur nichtnegative reelle Zahlen auftreten, also W(f)=[0,∞[W(f)=[0,\infty [.

Spezialfall R2\R^2

Für Funktionen f:R2→Rf: \R^2\to\R weicht man von der indizierten Tupelschreibweise ab und benutzt auch z=f(x,y)z=f(x,y) anstelle von y=f(x1,x2)y=f(x_1,x_2).
 
 

Jede mathematische Formel in einem Buch halbiert die Verkaufszahl dieses Buches.

Stephen Hawking

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analysis