Grenzwerte

Analog zu reellen Funktionen kann man bei Funktionen mehrerer Veränderlicher den Grenzwert definieren.
Eine Funktion f:Rn→Rf:\Rn\to \R sei in der Umgebung eines Punktes x0=(x10,x20,…,xn0)x^0=(x_1^0,x_2^0,\dots,x_n^0) definiert, wobei ff an der Stelle x0x^0 selbst nicht definiert sein muss.
ff hat an der Stelle x0x^0 den Grenzwert gg, geschrieben
lim⁡x→x0f(x)=g\lim_{x\to x^0} f(x)=g,
wenn zu jedem ϵ>0\epsilon>0 ein δ>0\delta>0 existiert, so dass für alle xx aus ∣∣x−x0∣∣<δ||x-x^0||<\delta auch ∣f(x)−g∣<ϵ|f(x)-g|<\epsilon folgt.
Analog zu Satz 5225E gilt:
 
 

Satz 165P (Zusammenhang zwischen Folgen- und Funktionsgenzwert)

Eine Funktion f:Rn→Rf:\Rn\to \R sei in der Umgebung eines Punktes x0=(x10,x20,…,xn0)x^0=(x_1^0,x_2^0,\dots,x_n^0) definiert, wobei ff an der Stelle x0x^0 selbst nicht definiert sein muss.
Es gilt lim⁡x→x0f(x)=g\lim_{x\to x^0} f(x)=g genau dann, wenn für jede Punktfolge (xk)(x^k) aus dem Definitionsbereich D(f)D(f) mit xk≠x0x^k\neq x^0 und lim⁡k→∞xk=x0\lim_{k\to\infty}x^k=x^0 gilt: lim⁡k→∞f(xk)=g\lim_{k\to\infty}f(x^k)=g.
Die Grenzwertsätze für reelle Funktionen (Satz 5227L) lassen sich leicht für Funktionen mehrerer Veränderlicher verallgemeinern.

Beispiele

Für die Funktion f(x1,x2)=x12+x22f(x_1,x_2)=x_1^2+x_2^2 aus Beispiel 165O gilt lim⁡xi→xi0x12+x22=(x10)2+(x20)2=f(x0)\lim_{x_i\to x_i^0} x_1^2+x_2^2= (x_1^0)^2+(x_2^0)^2=f(x^0). Der Grenzwert der Funktion stimmt also mit dem Funktionswert an der Stelle x0x^0 überein.

Beispiel 165Q

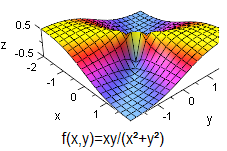
f2.png
Die Funktion f(x,y)=xyx2+y2f(x,y)=\dfrac{xy}{x^2+y^2} ist an der Stelle (x10,x20)=(0,0)(x_1^0,x_2^0)=(0,0) nicht definiert.
Für die Folge (xk)=(1k,1k)(x^k)=\braceNT{\dfrac 1 k ,\dfrac 1 k}, die für k→∞k\to\infty gegen (0,0) strebt, ist f(xk)=12f(x^k)=\dfrac 1 2.
Ist man nun versucht, lim⁡x→(0,0) xyx2+y2=12\lim_{x\to(0,0)}\, \dfrac{xy}{x^2+y^2}=\dfrac 1 2 anzunehmen, so wird man durch die Folge (xk)=(1k,ck)(x^k)=\braceNT{\dfrac 1 k ,\dfrac c k} (c≠0c\ne 0 ist eine konstante reelle Zahl) schnell umgestimmt. Denn es gilt:
f(xk)=ck21k2+c2k2f(x^k)=\dfrac {\dfrac c {k^2}} {\dfrac 1 {k^2}+\dfrac {c^2}{k^2}} =c1+c2=\dfrac c {1+c^2}
Diese Ausdruck kann beliebig viele verschiedene Werte annehmen, daher existiert der Funktionsgrenzwert von ff an der Stelle (0,0) nicht.

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mehrdimensionale Analysis