Färbung von Graphen
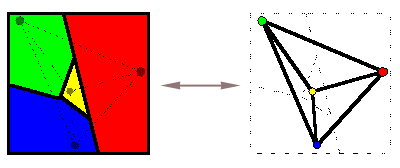
Darstellung einer kartographischen Färbung als Graph
Eine Färbung eines ungerichteten Graphen ordnet jedem Knoten bzw. jeder Kante im Graphen eine Farbe zu.
In der Graphentheorie beschäftigt man sich meist nur mit sogenannten "zulässigen" oder "gültigen" Färbungen (siehe unten), und versucht, Algorithmen zu entwickeln, die für einen vorgegebenen Graphen eine gültige Färbung mit möglichst wenig Farben finden. Probleme aus der diskreten Mathematik, aber auch außermathematische Fragestellungen lassen sich manchmal in ein Färbungsproblem übersetzen, daher ist die Existenz oder Nichtexistenz solcher Algorithmen auch außerhalb der Graphentheorie von Interesse.
Knotenfärbungen
Ist = ein ungerichteter Graph ohne Mehrfachkanten und eine Abbildung von in die Menge der natürlichen Zahlen , so nennt man eine Knotenfärbung von . Man nennt gültig oder zulässig, falls für je zwei beliebige benachbarte Knoten und gilt ≠ und sagt ist k-knotenfärbbar, falls es eine gültige Knotenfärbung von gibt, so dass für alle aus gilt: <. Das kleinste , für das -knotenfärbbar ist, nennt man die ""chromatische Zahl"" oder die ""Knotenfärbungszahl"" des Graphen und wird meist mit bezeichnet.
Eine zulässige Knotenfärbung eines Graphen ist eine Partition seiner Knotenmenge in unabhängige Mengen (eine Teilmenge der Knotenmenge eines Graphen heißt unabhängig, falls sie keine zwei benachbarten Knoten enthält).
Kantenfärbungen
Ist = ein ungerichteter Graph ohne Mehrfachkanten und eine Abbildung von in die Menge der natürlichen Zahlen , so nennt man eine Kantenfärbung von . Man nennt gültig oder zulässig, falls für je zwei beliebige benachbarte Kanten und gilt ≠ und sagt ist k-kantenfärbbar, falls es eine gültige Kantenfärbung von gibt, so dass für alle aus gilt: <. Das kleinste , für das -kantenfärbbar ist, nennt man den ""chromatischer Index"" oder die ""Kantenfärbungszahl"" des Graphen und wird meist mit bezeichnet.
Die Kantenfärbung eines Graphen lässt sich als Knotenfärbung des Kantengraphen betrachten. Daraus folgt dass .
Der Satz von Vizing besagt, dass der chromatische Index eines Graphen mindestens so groß wie sein Maximalgrad aber höchstens eins größer als dieser ist, also formal:
Obwohl der Maximalgrad leicht zu bestimmen ist und der chromatische Index nur einen von zwei möglichen Werten annehmen kann, ist das Problem, für einen gegebenen Graphen genau diesen einen Wert zu bestimmen, ebenfalls NP-schwer.
Der allgemeine Fall
Die Bestimmung der chromatischen Zahl eines Graphen ist NP-schwer, das heißt, dass es - aus Sicht der Komplexitätstheorie - vermutlich keinen Algorithmus gibt, der dieses Problem effizient löst.
Der zur Zeit praktisch beste Algorithmus beruht auf einem Spalten-Generierungs-Ansatz (siehe Literatur). Weiterhin gibt es viele Färbungsheuristiken, die nach bestimmten Methoden gute Färbungen suchen und somit im Erfolgsfall eine obere Schranke für die chromatische Zahl liefern.
Spezialfälle
Der Vier-Farbensatz besagt, dass die chromatische Zahl eines planaren Graphen höchstens 4 ist. Trotzdem ist auch für planare Graphen das Bestimmen der chromatischen Zahl NP-schwer.
Das Entscheidungsproblem, ob ein gegebener Graph bipartit ist, besitzt lineare Zeitkomplexität, und ist zum Beispiel mit Tiefensuche lösbar. (Bipartite Graphen sind genau die Graphen mit chromatischer Zahl höchstens 2.)
Für perfekte Graphen existieren Polynomialzeitalgorithmen zur Berechnung der chromatischen Zahl.
Weitere Sätze
Der Greedy-Algorithmus liefert als obere Schranke für die chromatische Zahl eines Graphen den Maximalgrad des Graphen plus 1. Beispiele, die zeigen, dass diese Abschätzung bestmöglich ist, sind Kreise ungerader Länge und vollständige Graphen. Der Satz von Brooks zeigt aber, dass dies auch die einzigen Beispiele sind. Für jeden zusammenhängenden Graphen, der keine Kreise ungerader Länge enthält oder nicht vollständig ist, ist seine chromatische Zahl stets kleiner oder gleich dem Maximalgrad des Graphen.
Anwendungen
Stundenplanprobleme lassen sich als Graphfärbungsprobleme formulieren: Die Knoten des Graphen sind dabei die zu platzierenden Veranstaltungen, und eine Kante wird zwischen zwei Veranstaltungen eingefügt, die nicht gleichzeitig stattfinden können (in der Schule wären das z.B. Stunden, die von demselben Lehrer unterrichtet werden sowie Stunden in derselben Klasse). Die möglichen Farben entsprechen den zuteilbaren Zeitfenstern.
In gleicher Weise können beispielsweise Register-Zuweisungs-Probleme in Prozessoren, Bandbreiten-Zuweisung-Probleme und auch viele andere Probleme aus der Mathematik als Graphenfärbungsprobleme formuliert werden.
Literatur
- Reinhard Diestel: Graphentheorie. Springer-Verlag, Heidelberg, Deutschland, 2000. ISBN-3-540-67656-2.
Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.
Leopold Kronecker
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Färbung (Graphentheorie)
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе