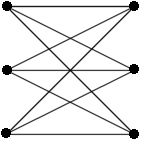
Bipartiter Graph

487_Graph_K3_3.png
K3,3K_{3,3}: vollständiger bipartiter Graph mit 3 Knoten pro Teilmenge
Ein einfacher Graph G=(V,E)G=(V,E) (V Menge der Knoten, E Menge der Kanten) heißt in der Graphentheorie bipartit (auch paar), falls sich seine Knoten in zwei disjunkte Teilmengen AA und BB aufteilen lassen, sodass zwischen den Knoten innerhalb beider Teilmengen keine Kanten verlaufen. Das heißt für eine Kante {v,w}∈E\{v,w\} \in E gilt entweder v∈Av \in A und w∈Bw \in B oder aber w∈Aw \in A und v∈Bv \in B. Die Menge {A, BA,\, B} bezeichnet man dann als Bipartition des Graphen GG.
Der Graph GG heißt vollständig bipartit, falls eine Bipartition {A,B}\{A,B\} existiert, für die für jedes Paar (a,b)(a,b) mit a∈Aa \in A und b∈Bb \in B die Kante {a,b}\{a,b\} zu EE gehört (d.h. jeder Knoten aus AA ist mit jedem Knoten aus BB verbunden, wie in der Graphik rechts zu sehen). Einen solchen Graphen bezeichnet man auch als Km,nK_{m,n}, wobei mm und nn die Anzahl der Knoten von AA bzw. BB sind.

Folgerungen

Die Teilmengen AA und BB sind also schon nach Definition stabile Mengen und die Bipartition impliziert eine mögliche 2-Färbung des Graphen. Umgekehrt sind alle 2-färbbaren Graphen bipartit.
Für bipartite Graphen lassen sich viele Grapheneigenschaften mit weniger Aufwand berechnen als dies im allgemeinen Fall möglich ist.
Mit einem einfachen Algorithmus, der auf Tiefensuche basiert, lässt sich in linearer Zeit bestimmen, ob ein Graph bipartit ist, und eine gültige Partition bzw. 2-Färbung ermitteln.

Eigenschaften

  • Die Paarungszahl entspricht der Knotenüberdeckungszahl.
  • Mit dem Algorithmus von Hopcroft und Karp lässt sich in O(nm)O(\sqrt{nm}) eine größte Paarung finden und darüber auch die Stabilitätszahl bestimmen.
  • Der chromatische Index entspricht seinem Maximalgrad. Eine gültige Kantenfärbung lässt sich in O(nm) bestimmen.
  • Ein regulärer bipartiter Graph besitzt ein perfektes Matching.
  • Ein Graph ist genau dann bipartit, wenn er keinen Kreis ungerader Länge enthält.
 
 

Die Mathematik muß man schon deswegen studieren, weil sie die Gedanken ordnet.

M. W. Lomonossow

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Bipartiter Graph aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Graphentheorie