Teilgraphen und Minoren

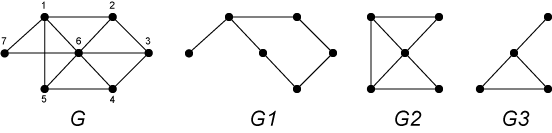
Bei der Untersuchung von Grapheneigenschaften schließt man häufiger von lokalen auf globale Eigenschaften von Graphen und umgekehrt. Um derartige Vorgänge besser beschreiben zu können, definiert man geeignete Relationen zwischen Graphen und lokalen Gebieten innerhalb dieser Graphen. Besonders wichtig sind dabei Teilgraphenbeziehungen. Die Begriffe Teilgraph und Untergraph sind Spezialfälle der entsprechenden allgemeineren Begriffe Teil-Struktur und Unter-Struktur aus der Modelltheorie. Eine Unter-Struktur ist anschaulich gesehen ein Ausschnitt aus einer Struktur, bei der alle Beziehungen zwischen den Elementen (bzw. Knoten) erhalten bleiben. Beispiel siehe unten: G2, G3 sind Untergraphen von G aber G1 ist kein Untergraph sondern nur ein Teilgraph von G. In Teil-Strukturen können also zusätzlich noch Beziehungen zwischen den Elementen wegfallen. Jede Unter-Struktur ist eine Teil-Struktur aber nicht umgekehrt. Im folgenden werden beide Begriffe für Graphen näher definiert.

Definitionen

Teilgraph

G_{1}

(V_{1},E_{1})

heißt Teilgraph oder Subgraph von

G_{2}

(V_{2},E_{2})

, falls

V_{1}

Teilmenge von

V_{2}

, also

V_1\subseteq V_2

und

in Graphen ohne Mehrfachkanten $E_{1}$ Teilmenge von $E_{2}$ ist, $E_1\subseteq E_2$ ,
in ungerichteten Graphen mit Mehrfachkanten $E_1(v)\subseteq E_2(v)$ für alle zweielementigen Teilmengen $v$ von $V_{2}$ , also $v:=\chooseNT{V_2}{2}$ , gilt, wobei $E_{1/2}(v)$ die Menge der Kanten zwischen den Knoten aus $v$ ist,
in gerichteten Graphen mit Mehrfachkanten $E_1(v)\subseteq E_2(v)$ für alle Teilmengen $v$ aus dem kartesischen Produkt $V_{2}$ x $V_{2}$ gilt.

Umgekehrt heißt

G_{2}

Supergraph oder Obergraph von

G_{1}

Bei einem knotengewichteten bzw. kantengewichteten Graph

G_{2}

wird von einem Teilgraph

G_{1}

zudem verlangt, dass die Gewichtsfunktion

g_{1}

von

G_{1}

kompatibel zu der Gewichtsfunktion

g_{2}

von

G_{2}

ist, d.h. für jeden Knoten

v

bzw. für jede Kante

e

von

G_{2}

gilt

g_1(v) = g_2(v)

bzw.

g_1(e) = g_2(e)

Untergraph bzw. Induzierter Teilgraph

Gilt zusätzlich:

in Graphen ohne Mehrfachkanten, $E_1 = E_2 \cap \chooseNT{V_1}{2}$ , d.h. $G_{1}$ enthält alle Kanten zwischen den Knoten in $V_{1}$ , die auch in $G_{2}$ vorhanden sind.
in ungerichteten Graphen mit Mehrfachkanten, $E_1(v) = E_2(v) \cap \chooseNT{V_1}{2}$ für alle zweielementigen Teilmengen $v$ von $V_{2}$ ,
in gerichteten Graphen mit Mehrfachkanten, $E_1(v) = E_2(v) \cap \chooseNT{V_1}{2}$ für alle $v$ aus dem kartesischen Produkt $V_{2}$ x $V_{2}$ ,

so bezeichnet man

G_{1}

auch als den durch

V_{1}

induzierten Teilgraph von

G_{2}

und notiert diesen auch mit

G_{2}

[

V_{1}

]

Bemerkungen:

Induzierte Teilgraphen sind immer eindeutig durch die entsprechende Knotenmenge festgelegt.
Besonders wichtige Teilgraphen entstehen durch das Weglassen von Knoten bzw. Kanten. Sei der Graph G(V,E) gegeben, dann bezeichnet $G\setminus A, A \subseteq V$ den Graphen, der durch Weglassen der Knoten aus A und aller mit diesen Knoten inzidenten Kanten entsteht. Die so entstehenden Teilgraphen sind immer induzierte Teilgraphen!

Beispiele

In der folgenden Abbildung sind die Graphen

G_{1},\, G_{2},\, G_{3}

Teilgraphen von

G

, wobei aber nur

G_{2}

und

G_{3}

induzierte Teilgraphen sind.

G_{3}

entsteht dabei aus

G

durch Weglassen der Knoten 1,3,7 und ihrer inzidenten Kanten.

Minor

Ein Graph

G_{1}

wird Minor des Graphen

G_{2}

genannt, falls

G_{1}

isomorph zu einem durch Knotenverschmelzung entstandenen Untergraphen von

G_{2}

ist. Knotenverschmelzung bedeutet hier, dass zwei adjazente (benachbarte) Knoten

V_{1}

und

V_{2}

unter Entfernung einer zu diesen beiden Knoten inzidenten Kante zu einem Knoten

V_{12}

„verschmolzen“ werden, wobei alle restlichen Kanten beibehalten werden.

Zum Beispiel ist in der folgenden Abbildung

G

1 ein Minor von

G

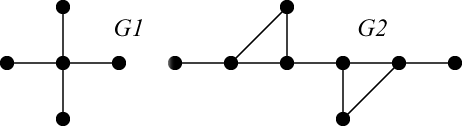
G1 ist Minor zu G2

Die Minor-Beziehung definiert eine partielle Ordnungsrelation auf den Isomorphie-Klassen von Graphen.

Robertson und Seymour haben gezeigt, dass für jede unendliche Folge

G_{1},G_{2}

,... von endlichen Graphen stets Indizes

i

und

j

mit

i < j

existieren, so dass

G_{i}

ein Minor von

G_{j}

ist.

Siehe auch: Satz von Kuratowski, Satz von Robertson und Seymour

Ein guter mathematischer Scherz ist immer besser als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen.

John Edensor Littlewood

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Teilgraphen und Minoren aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе

Datenschutzerklärung