Kartesisches Produkt

Das kartesische Produkt zweier Mengen ist die Menge aller geordneten Paare mit Elementen aus den einzelnen Mengen.
A×B={(a,b)∣ a∈A∧b∈B}A\cross B =\{(a,b)|\space a\in A \and b\in B\}
Eine andere Bezeichnung für das kartesische Produkt ist auch Produktmenge.
Wir können die Definition des kartesischen Produkts sofort unter Benutzung von n-Tupeln für n Mengen erweitern:
A1×…×An:={(a1,…,an)∣ a1∈A1∧…∧an∈An}A_1\cross\ldots\cross A_n := \{(a_1,\ldots,a_n)|\space a_1\in A_1 \and \ldots\and a_n\in A_n\}.
 
 

Beispiel

Sei A={1;3}A=\{1; 3\} und B={1;2}B=\{1;2\} gegeben. Dann ist
A×B={(1;1) (1;2) (3;1) (3;2)}A\cross B=\{(1;1)\, (1;2)\, (3;1)\, (3;2)\}
und
B×A={(1;1) (1;3) (2;1) (2;3)}B\cross A=\{(1;1)\, (1;3)\, (2;1)\, (2;3)\}
KProdukt.png
Es ist also A×B≠B×AA\cross B\neq B\cross A und damit zeigt dieses Beispiel, dass das kartesische Produkt für Mengen nicht kommutativ ist.
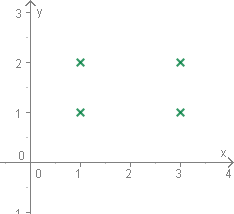
Man kann sich kartesische Produkte im Koordinatensystem veranschaulichen. Die nebenstehende Grafik zeigt die Menge A×BA\cross B.

Das Zusammenspiel des kartesischen Produktes mit den den anderen Mengenoperationen klärt:

Satz 12MP (Eigenschaften des kartesischen Produktes)

Für Mengen AA, BB, CC und DD gilt:
  1. (A∪B)×C=(A×C)∪(B×C)(A\cup B)\cross C=(A\cross C)\cup (B\cross C) und A×(B∪C)=(A×B)∪(A×C)A\cross (B\cup C)=(A\cross B)\cup (A\cross C)
  2. (A∩B)×C=(A×C)∩(B×C)(A\cap B)\cross C=(A\cross C)\cap (B\cross C) und A×(B∩C)=(A×B)∩(A×C)A\cross (B\cap C)=(A\cross B)\cap (A\cross C)
  3. (A∖B)×C=(A×C)∖(B×C)(A\setminus B)\cross C=(A\cross C)\setminus (B\cross C) und A×(B∖C)=(A×B)∖(A×C)A\cross (B\setminus C)=(A\cross B)\setminus (A\cross C)
  4. (A×B)∪(C×D)⊆(A∪C)×(B∪D)(A\cross B)\cup (C\cross D)\subseteq (A\cup C)\cross(B\cup D) (A×B)∩(C×D)=(A∩C)×(B∩D)(A\cross B)\cap (C\cross D)= (A\cap C)\cross(B\cap D)
  5. A×B=∅  ⟺  A=∅∨B=∅A\cross B=\emptyset\iff A=\emptyset\or B=\emptyset
  6. A⊆B∧C⊆D  ⟹  (A×C)⊆(B×D)A\subseteq B\and C\subseteq D\implies (A\cross C)\subseteq (B\cross D)

Das ist ein Mittel, das Paradies nicht zu verfehlen: auf der einen Seite einen Mathematiker, auf der anderen einen Jesuiten; mit dieser Begleitung muß man seinen Weg machen, oder man macht ihn niemals.

Friedrich der Große

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre