Planarer Graph
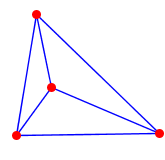
Planare Zeichnung des
Ein planarer Graph (auch plättbarer Graph) ist in der Graphentheorie ein Graph, der auf einer Ebene mit Punkten für die Knoten und Linien für die Kanten dargestellt werden kann, so dass sich die Kanten nicht schneiden.
Der Satz von Kuratowski gibt eine weitere Charakterisierung von planaren Graphen und erlaubt die Beantwortung der Frage nach der Plättbarkeit von Graphen.
Eine konkrete Darstellung eines Graphen in der Ebene wird auch Einbettung genannt. Ein ebener Graph ist ein in die Ebene eingebetteter Graph. Durch die Einbettung wird die Ebene in zusammenhängende Gebiete geteilt, die von den Kanten des Graphen begrenzt werden. Die begrenzenden Kanten eines Gebietes bilden seinen Rand. Das Gebiet um den Graphen herum wird auch äußeres Gebiet genannt. Die Einbettung kann auch auf einer Kugeloberfläche stattfinden. Umgekehrt ist auch jeder auf einer Kugel kreuzungsfrei darstellbare Graph planar.
Zwei Einbettungen sind äquivalent, wenn es eine isomorphe Abbildung zwischen den Rändern ihrer Gebiete gibt. Es lässt sich zeigen, dass für jeden planaren Graph auch eine Einbettung existiert, bei der die Kanten Geraden sind.
Ein Graph heißt maximal planar oder Dreiecksgraph, wenn er planar ist und ihm keine Kante hinzugefügt werden kann, ohne dass dadurch seine Planarität verloren geht.
Ein Graph heißt fast planar oder kritisch planar, wenn der Graph durch Entfernen eines beliebigen Knotens planar wird. Bsp.: ist fast planar.
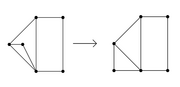
Beispiel eines kreisartig plättbaren Graphen
Ein Graph heißt kreisartig planar, wenn er sich so in Ebene einbetten lässt, dass alle seine Ecken auf dem Rand ein und desselben Gebiets liegen.
Die Planarität eines Graphen lässt sich mit verschiedenen Algorithmen in linearer Zeit testen. Allerdings sind diese Algorithmen nicht einfach zu implementieren.
Verbindung zu anderen Graph-Eigenschaften
In einem zusammenhängenden planaren Graphen gilt nach dem eulerschen Polyedersatz stets:
Knotenanzahl + Gebietsanzahl = Kantenanzahl + 2
Aus dieser Eigenschaft folgt, dass planare Graphen in Bezug auf die Knotenanzahl nur linear viele Kanten haben können.
Ist ein planarer Graph 3-fach zusammenhängend, so sind alle seine Einbettungen äquivalent.
Der Vier-Farben-Satz besagt, dass sich planare Graphen mit 4 Farben färben lassen. Dreiecksfreie planare Graphen sind 3-färbbar.
Ein planarer Graph kann höchstens 5-fach zusammenhängend sein.
Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.
Karl Menger
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Planarer Graph
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе