Majoranten und Minoranten

Sei MM eine teilweise geordnete Menge mit der Ordnung ≤\leq. Für eine nichtleere Teilmenge A⊆MA\subseteq M heißt ein Element s∈Ms\in M obere Schranke von AA, wenn a≤sa\leq s für alle a∈Aa\in A gilt. Analog heißt ss untere Schranke von AA, wenn s≤as\leq a für alle a∈Aa\in A gilt.
Existieren die obere (untere) Schranke, so heißt die Menge nach oben (unten) beschränkt.
Die Menge aller oberen Schranken von AA heißt Majorante von AA (Bezeichnung: Ma⁡(A)\Ma(A)) und die Menge aller unteren Schranken heißt Minorante von AA und wird mit Mi⁡(A)\Mi(A) bezeichnet.
Es ist also
Ma⁡(A)={x∈M ∣ a≤x∀a∈A}\Ma(A)=\{x\in M\, |\, a\leq x\forall a\in A\}
Mi⁡(A)={x∈M ∣ x≤a∀a∈A}\Mi(A)=\{x\in M\, |\, x\leq a\forall a\in A\}.
 
 

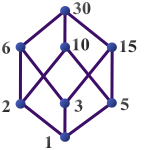
Beispiel

OrdT30.png
Betrachten wir die Zahl 30 und ihre Teiler mit der Ordnung bzgl. der Teilbarkeit als Ordnung, und sei A=A={2; 5}. Dann ist Mi⁡(A)=\Mi(A)={1} und Ma⁡(A)=\Ma(A)={10; 30}.

Satz 1601 (Eigenschaften von Minorante und Majorante)

Sei MM eine teilweise geordnete Menge mit der Ordnung ≤\leq. Für nichtleere Teilmengen A,B⊆MA,B\subseteq M gilt dann:
  1. A⊆Ma⁡(Mi⁡(A))A\subseteq \Ma(\Mi(A)) und A⊆Mi⁡(Ma⁡(A))A\subseteq \Mi(\Ma(A))
  2. A⊆B  ⟹  A\subseteq B\implies Ma⁡(B)⊆Ma⁡(A)\Ma(B)\subseteq \Ma(A) und Mi⁡(B)⊆Mi⁡(A)\Mi(B)\subseteq \Mi(A)
  3. Mi⁡(Ma⁡(Mi⁡(A)))=Mi⁡(A)\Mi(\Ma(\Mi(A)))=\Mi(A) und Ma⁡(Mi⁡(Ma⁡(A)))=Ma⁡(A)\Ma(\Mi(\Ma(A)))=\Ma(A).
  4. Für a,b∈Ma,b\in M gilt: a≤b  ⟺  Mi⁡(a)⊆Mi⁡(b)a\leq b\iff \Mi(a)\subseteq \Mi(b)   ⟺  Ma⁡(b)⊆Ma⁡(a)\iff \Ma(b)\subseteq \Ma(a)

Beweis

(i) Sei a∈Aa\in A und x∈Mi⁡(A)x\in \Mi(A) beliebig. Dann ist x≤yx\leq y für alle y∈Ay\in A speziell auch x≤ax\leq a. Da xx beliebig gewählt war, gilt dies für alle x∈Mi⁡(A)x\in \Mi(A) und damit ist a∈Ma⁡(Mi⁡(A))a\in \Ma(\Mi(A)), also A⊆Ma⁡(Mi⁡(A))A\subseteq \Ma(\Mi(A)). Analog zeigt man A⊆Mi⁡(Ma⁡(A))A\subseteq \Mi(\Ma(A)).
(ii) Sei x∈Ma⁡(B)x\in \Ma(B), dann ist x≥bx\geq b für alle b∈Bb\in B und wegen A⊆BA\subseteq B auch x≥ax\geq a für alle a∈Aa\in A, also: x∈Ma⁡(A)x\in \Ma(A). Mi⁡(B)⊆Mi⁡(A)\Mi(B)\subseteq \Mi(A) geht analog.
(iii) Ersetzen wir in (i) AA durch Ma⁡(A)\Ma(A), erhalten wir: Ma⁡(A)⊆Ma⁡(Mi⁡(Ma⁡(A)))\Ma(A)\subseteq \Ma(\Mi(\Ma(A))). Nach (i) ist A⊆Mi⁡(Ma⁡(A))A\subseteq \Mi(\Ma(A)) und mit (ii) gilt dann Ma⁡(Mi⁡(Ma⁡(A)))⊆Ma⁡(A)\Ma(\Mi(\Ma(A)))\subseteq \Ma(A). Damit haben wir Ma⁡(Mi⁡(Ma⁡(A)))=Ma⁡(A)\Ma(\Mi(\Ma(A)))=\Ma(A).
Mi⁡(Ma⁡(Mi⁡(A)))=Mi⁡(A)\Mi(\Ma(\Mi(A)))=\Mi(A) kann man auf die gleiche Art aus (i) und (ii) herleiten.
(iv) Sei a≤ba\leq b; x∈Mi⁡(a)  ⟹  x≤a≤bx\in\Mi(a)\implies x\leq a\leq b, also x∈Mi⁡(b)x\in\Mi(b) und Mi⁡(a)⊆Mi⁡(b)\Mi(a)\subseteq \Mi(b); x∈Ma⁡(b)  ⟹  b≥a≥xx\in\Ma(b)\implies b\geq a\geq x, also x∈Ma⁡(a)x\in\Ma(a) und Ma⁡(b)⊆Ma⁡(a)\Ma(b)\subseteq \Ma(a).
Mi⁡(a)⊆Mi⁡(b)\Mi(a)\subseteq \Mi(b)   ⟹  a∈Mi⁡(b)\implies a\in \Mi(b)   ⟹  a≤b\implies a\leq b.
Ma⁡(b)⊆Ma⁡(a)\Ma(b)\subseteq \Ma(a)   ⟹  b∈Ma⁡(a)\implies b\in \Ma(a)   ⟹  b≥a\implies b\geq a.□\qed

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ordnungstheorie