Isotone Abbildungen

Seien MM und NN zwei teilweise geordnete Mengen und f:M→Nf:M\rightarrow N eine Abbildung. ff heißt isoton oder ordnungserhaltend genau dann, wenn für alle a,b∈Ma,b\in M gilt: a≤b  ⟹  f(a)≤f(b)a\leq b\implies f(a)\leq f(b).
Die Abbildung heißt antiton, wenn gilt: a≤b  ⟹  f(a)≥f(b)a\leq b\implies f(a)\geq f(b).
ff ist ein Ordnungsisomorphismus zwischen MM und NN genau dann, wenn ff bijektiv ist und sowohl ff als auch die Umkehrabbildung f −1f^{\, \me} isoton sind. Die beiden Mengen MM und NN heißen dann auch ordnungsisomorph. Beispiel 160G lässt sich damit als Ordnungsisomorphismus deuten.
Iso.png
Eine isotone Bijektion muss nicht notwendigerweise eine isotone Umkehrung haben, daher ist diese Forderung in der Definition des Ordnungsisomorphismus wesentlich.
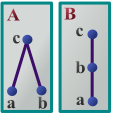
Für die nebenstehenden Hassediagramme ist die identische Abbildung id⁡:A→B\id:A\rightarrow B (a↦aa\mapto a, b↦bb\mapto b, c↦cc\mapto c) isoton. Die Umkehrung ist nicht isoton, da a≤ba\leq b in BB; jedoch aa und bb in AA unvergleichbar sind.
Für linear geordnete Mengen gilt jedoch:
 
 

Satz 160F (Isotone Bijektionen als Ordnungsisomorphismen linear geordneter Mengen)

Seien MM und NN linear geordnete Mengen und f:M→Nf:M\rightarrow N eine isotone Bijektion. Dann ist die Umkehrabbildung von ff isoton und damit ist ff ein Ordnungsisomorphismus.

Beweis

Seien n1,n2∈Nn_1,n_2\in N mit n1≤n2n_1\leq n_2 und m1=f −1(n1)m_1=f^{\, \me}(n_1) sowie m2=f −1(n2)m_2=f^{\, \me}(n_2). Wir müssen zeigen, dass dann m1≤m2m_1\leq m_2 gilt. Angenommen m1≰m2m_1\nleq m_2, dann ist m2<m1m_2<m_1, da die Ordnung linear ist und wegen der Isotonie und Bijektivität von ff gilt: f(m2)<f(m1)f(m_2)<f(m_1), d.h. n2<n1n_2<n_1, im Widerspruch zu n1≤n2n_1\leq n_2, womit m1≤m2m_1\leq m_2 gezeigt ist. □\qed

Hochtechnologie ist im wesentlichen mathematische Technologie.

Enquete-Kommission der Amerikanischen Akademie der Wissenschaften

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ordnungstheorie