Verbände

Sei MM eine teilweise geordnete Menge mit der Ordnung ≤\leq. MM heißt verbandsgeordnete Menge oder Verband, wenn folgende Eigenschaften gelten:
  1. Zu je zwei Elementen a,b∈Ma,b\in M existiert das Infimum inf⁡(a,b)\inf(a,b)
  2. Zu je zwei Elementen a,b∈Ma,b\in M existiert das Supremum sup⁡(a,b)\sup(a,b)
Damit besitzen dann auch endliche Teilmengen von MM Infimum und Supremum (Beweis durch vollständige Induktion).
Ist MM selbst endlich, so besitzt MM sowohl ein Minimum, das Ordnungsnull heißt, als auch ein Maximum, welches Ordnungseins genannt wird.
Jede kettengeordnete Menge ist ein Verband. Für jede zweielementige Teilmenge existieren dann Minimum und Maximum und sind mit dem Infimum und Supremum identische.

Beispiele

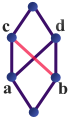
Nv1.png
Das nebenstehende Hassediagramm veranschaulicht einen Verband (ohne hellrote Linie). Es gilt d=sup⁡(a,b)d=\sup(a,b) und a=inf⁡(c,d)a=\inf(c,d).
Nimmt man die hellrote Linie hinzu, so ist die Verbandsstruktur zerstört, da sowohl cc als auch dd obere Schranken von aa und bb sind. Wegen ihrer Unvergleichbarkeit existiert jedoch d=sup⁡(a,b)d=\sup(a,b) nicht.

Algebraische Schreibweise

Um Gesetze mit Supremum und Infimum ohne tiefe Klammerung formulieren zu können, werden in Verbänden die Symbole ∨ \vsup \, für Supremum und ∧ \vinf \, für Infimum verwendet. Wir definieren:
a∨b:=sup⁡(a,b) a\vsup b:=\sup(a,b)\,
a∧b:=inf⁡(a,b)a\vinf b:=\inf(a,b)
 
 

Es gibt Dinge, die den meisten Menschen unglaublich erscheinen, die nicht Mathematik studiert haben.

Archimedes

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Algebra