Mengenverbände

Sei MM eine beliebige Menge und P(M)\Pow(M) ihre Potenzmenge. Unter einem Mengenverband M⊆P(M)\sb M\subseteq \Pow(M) versteht man eine Teilmenge der Potenzmenge, die mit zwei Mengen AA und BB auch ihre Vereinigung A∪BA\cup B und ihren Durchschnitt A∩BA\cap B enthält. Ein Mengenverband ist also bezüglich der endlichern Durchschnitts- und Vereinigungsbildung abgeschlossen.
Jeder Mengenverband ist bzgl. der Inklusion ⊆\subseteq ein Verband und es gilt:
sup⁡(A,B)=A∪B\sup(A,B)=A\cup B und inf⁡(A,B)=A∩B\inf(A,B)=A\cap B.
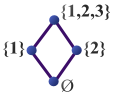
TM3Nv.png
Ein Mengensystem, das bezüglich der Inklusion ⊆\subseteq einen Verband bildet, muss nicht notwendigerweise ein Mengenverband sein (siehe Beispiel 160H und nebenstehendes Hassediagramm).

Beispiele

Potenzmenge

Die Potenzmenge P(M)\Pow(M) einer beliebigen Menge MM bildet einen Mengenverband.
Das System aller endlichen Teilmengen von MM ist ein Mengenverband.

Metrische Räume

In einem metrischen Raum (X,d)(X,d) kann man auf vielerlei Weise Mengenverbände entdecken:

Gruppen

In einer Gruppe (G,∘)(G,\circ) bildet das System aller Untergruppen bezüglich der Inklusion einen Verband. Für zwei Untergruppen HH und FF ist dabei inf⁡(H,F)=H∩F\inf(H,F)=H\cap F (ist nach Satz 5210B wieder Gruppe). Das Supremum entspricht der von H∪FH\cup F erzeugten Untergruppe ⟨H∪F⟩\spo H\cup F\spc.
Es handelt sich hierbei im allgemeinen um keinen Mengenverband, da nicht notwendigerweise H∪F=⟨H∪F⟩H\cup F=\spo H\cup F\spc gilt.
 
 

Seit der Zeit der Griechen bedeutet "Mathematik" zu sagen, "Beweis" zu sagen.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ordnungstheorie