Vereinigung von Mengen

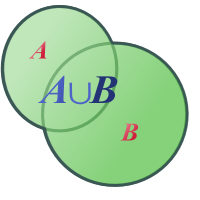
Vereinigung.png
Venndiagramm für die Vereinigung zweier Mengen
Die Vereinigung zweier Mengen ist die Menge, die diejenigen Elemente enthält, die wenigstens in einer der beiden Mengen enthalten ist, sie umfasst also die Elemente beider Mengen.
A∪B:={x∣ x∈A∨x∈B}A\cup B:= \{x|\, x\in A \or x\in B\}
oder für die Elemente
x∈A∪B  ⟺  x∈A∨x∈Bx\in A \cup B \iff x\in A \or x\in B

Satz 12MF (Eigenschaften der Vereinigung)

Für Mengen AA, BB und CC gilt:
  1. A∪B=B∪AA\cup B=B\cup A (Kommutativgesetz)
  2. (A∪B)∪C=A∪(B∪C)(A\cup B) \cup C=A\cup (B \cup C) (Assoziativgesetz)
  3. A∪A=AA\cup A = A (Idempotenz)
  4. A∪∅=AA\cup \emptyset = A
  5. A⊆A∪BA\subseteq A\cup B und B⊆A∪BB\subseteq A\cup B

Beweis

Der Beweis ergibt sich durch Zurückführung auf die aussagenlogischen Identitäten. □\qed
Der Zusammenhang zwischen Durchschnitt und Vereinigung wird durch folgende Gesetze hergestellt.

Satz 12MG (Zusammenhang zwischen Durchschnitt und Vereinigung)

Für Mengen AA, BB und CC gilt:
  1. Distributivgesetze
    A∪(B∩C)=(A∪B)∩(A∪C)A\cup (B \cap C) = (A\cup B) \cap (A\cup C)
    A∩(B∪C)=(A∩B)∪(A∩C)A\cap (B \cup C) = (A\cap B) \cup (A\cap C)
  2. Absorptionsgesetze
    A∩(A∪B)=A∪(A∩B)=AA\cap (A\cup B) = A\cup (A \cap B) = A
  3. Verträglichkeitsgesetz
    A∩B=A  ⟺  A∪B=BA\cap B=A \iff A\cup B=B
    A⊆B  ⟺  A∩B=A  ⟺  A∪B=BA\subseteq B \iff A\cap B=A \iff A\cup B=B

Beweis

(i) und (ii) rechnet man schnell über aussagenlogische Identitäten durch. Der Beweis des zweiten Teils ergibt sich dabei aus der aussagenlogischen Identität a  ⟹  b=a  ⟺  a∧ba\implies b = a\iff a\and b.
(iii) Sei A∩B=AA\cap B=A, dann gilt wegen der Absorptionsgesetze A∪B=(A∩B)∪B=BA\cup B=(A\cap B)\cup B=B. Die Umkehrung zeigt man analog. □\qed
 
 

Die Mathematik als Fachgebiet ist so ernst, daß man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.

Blaise Pascal

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre