Symmetrische Differenz

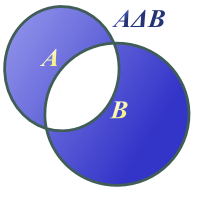
SymDiff.png
Venndiagramm zur symmetrischen Differenz
Die symmetrische Differenz zweier Mengen AA und BB ist definiert als
A Δ B:=(A∖B)∪(B∖A)A\space \Delta \space B:=(A\setminus B)\cup (B\setminus A).
Durch Umformungen (vgl. Satz 5910C) erhält man leicht die äquivalente Definition:
A Δ B:=(A∪B)∖(A∩B)A\space \Delta \space B:=(A\cup B)\setminus (A\cap B)
Die symmetrische Differenz zweier Mengen enthält also genau diejenigen Elemente, die in exakt einer Menge enthalten sind; also diejenigen Elemente, die in ihrer Vereinigung, aber nicht in ihrem Durchschnitt enthalten sind.

Satz 5524E (Eigenschaften der symmetrischen Differenz)

Für Mengen AA, BB und CC gilt:
  1. (A Δ B) Δ C=A Δ (B Δ C)(A\space\Delta\space B) \space\Delta\space C =A\space\Delta\space (B \space\Delta\space C) (Assoziativität)
  2. A Δ B=B Δ AA\space \Delta \space B= B\space \Delta \space A (Kommutativität)
  3. A Δ ∅=AA\space \Delta \space \emptyset = A und A Δ A=∅A\space \Delta \space A = \emptyset
 
 

Beweis

Durch Anwendung der Definition und etwas Rechnerei weist man diese Regeln schnell nach.
Die symmetrische Differenz entspricht der aussagenlogischen Operation der Kontravalenz, so dass deren Eigenschaften sich als Aussagen des obigen Satzes widerspiegeln. Besonders der Beweis der Assoziativität, der sich bei Zurückführung auf Vereinigung Durchschnitt und Differenz als langatmige Rechnerei darstellt, kann so wesentlich vereinfacht werden. □\qed
Satz 5218A zeigt, dass die symmetrische Differenz in der Potenzmenge eine Gruppenoperation ist.

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre