Differenz von Mengen

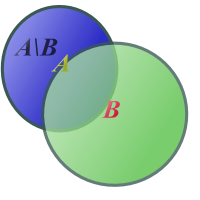
Diff.png
Venndiagramm zur Differenzmenge
Die Differenzmenge zweier Mengen enthält alle Elemente, die in der ersten Menge enthalten sind und nicht in der zweiten.
A∖B:={x∣x∈A∧x∉B}A\setminus B:= \{x| x\in A \and x\notin B\}
x∈A∖B  ⟺  x∈A∧x∉Bx\in A \setminus B \iff x\in A \and x\notin B

Satz 5910C (Eigenschaften der Mengendifferenz)

  1. A∖∅=AA\setminus \emptyset=A,
    A∖A=∅A\setminus A=\emptyset,
  2. A∖(A∖B)=A∩BA\setminus (A\setminus B)=A\cap B
  3. (A∩B)∖C=(A∖C)∩(B∖C)(A\cap B)\setminus C=(A\setminus C) \cap (B\setminus C),
    (A∪B)∖C=(A∖C)∪(B∖C)(A\cup B)\setminus C=(A\setminus C) \cup (B\setminus C),
  4. A∖(B∩C)=(A∖B)∪(A∖C)A\setminus (B \cap C) = (A\setminus B) \cup (A\setminus C)
    A∖(B∪C)=(A∖B)∩(A∖C)A\setminus (B \cup C) = (A\setminus B) \cap (A\setminus C) =(A∖B)∖C=(A∖C)∖B =(A\setminus B)\setminus C=(A\setminus C)\setminus B,
  5. A∖(B∖C)=(A∖B)∪(A∩C)A\setminus (B\setminus C)=(A\setminus B)\cup (A\cap C)
  6. A∖B⊆AA\setminus B \subseteq A
 
 

Beweis

Kann man schnell nachrechnen. □\qed

Mengenkomplement

Geht man von einer Grundmenge MM aus und betrachtet Operationen nur auf Teilmengen A⊆A\subseteq dieser Grundmenge, so definiert man
Ac:=M∖AA^c:=M\setminus A
also Mengenkomplement oder kurz Komplement.

Satz 16RH (Eigenschaften des Mengenkomplements)

  1. Mc=∅M^c=\OO,
    ∅c=M\emptyset^c=M,
  2. Acc=AA^{cc}=A
  3. (A∩B)c=Ac∪Bc(A\cap B)^c=A^c\cup B^c,
    (A∪B)c=Ac∩Bc(A\cup B)^c=A^c\cap B^c =Ac∖B=Bc∖A=A^c\setminus B=B^c\setminus A ,
  4. (A∖B)c=Ac∪B(A\setminus B)^c=A^c\cup B

Beweis

Die Behauptungen folgen direkt aus Satz 5910C. □\qed

So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre