Durchschnitt von Mengen

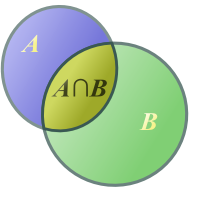
Durchschnitt.png
Venndiagramm für den Durchschnitt
Der Durchschnitt A∩BA\cap B zweier Mengen AA und BB ist als diejenige Menge definiert, die alle Elemente enthält, die in beiden Mengen vorhanden sind.
A∩B:={x∣ x∈A∧x∈B}A \cap B:=\{x|\, x\in A \and x\in B\}
oder für die Elemente
x∈A∩B  ⟺  x∈A∧x∈Bx\in A \cap B \iff x\in A \and x\in B
AA und BB heißen disjunkt, wenn ihr Durchschnitt die leere Menge ist (A∩B=∅A\cap B=\emptyset).
 
 

Satz 12ME (Eigenschaften des Durchschnitts)

Für Mengen AA, BB und CC gilt:
  1. A∩B=B∩AA\cap B=B\cap A (Kommutativgesetz)
  2. (A∩B)∩C=A∩(B∩C)(A\cap B) \cap C=A\cap (B \cap C) (Assoziativgesetz)
  3. A∩A=AA\cap A = A (Idempotenz)
  4. A∩∅=∅A\cap \emptyset = \emptyset
  5. A∩B⊆AA\cap B \subseteq A und A∩B⊆BA\cap B \subseteq B

Beweis

Den Beweis dieser Beziehung wird über die Elemente geführt unter Bezugnahme auf die entsprechenden aussagenlogischen Beziehungen. Dies soll am Kommutativgesetz exemplarisch vorgeführt werden: Wenn x∈A∩Bx\in A\cap B gilt x∈A∧x∈Bx\in A \and x\in B also - da ∧\and kommutativ ist - auch x∈B∧x∈Ax\in B \and x\in A. Damit haben wir x∈B∩Ax\in B\cap A, womit gezeigt ist A∩B⊆B∩AA\cap B\subseteq B\cap A. Die Umkehrung B∩A⊆A∩BB\cap A\subseteq A\cap B zeigt man analog. □\qed
Im Allgemeinen kann man die Beweise der Mengenbeziehungen auf aussagenlogische Identitäten reduzieren, daher werden wir die Beweise nur noch angeben, wenn sie etwas Neues enthalten.

Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.

Karl Menger

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre