Beispiele zum Infimum und Supremum in teilweise geordneten Mengen

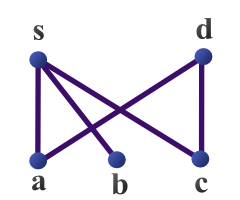
Sup.png
In der nebenstehenden Grafik ist das Hassediagramm einer teilweise geordneten Menge veranschaulicht. Die Menge {a,b}\{a,b\} besitzt mit ss ein Supremum. Die Menge {a,c}\{a,c\} besitzt kein Supremum, da die beiden oberen Schranken ss und dd kein Minimum besitzen. Die Menge {b,c}\{b,c\} besitzt kein Minimum, da die Minorante leer ist, gleiches gilt für {d,s}\{d,s\}, da es kein Element gibt, das kleiner als dd und ss ist.
 
 

Zahlen mit natürlicher Ordnung

Wegen der Vollständigkeit der reellen Zahlen besitzt jede nicht leere beschränkte Menge Supremum und Infimum.
Für zwei Zahlen (natürliche, ganze, rationale und reelle) sind Infimum und Supremum immer definiert und fallen mit dem Minimum und Maximum zusammen.

Kettengeordnete Mengen

Allgemein gilt für eine kettengeordnete Menge MM für zwei Elemente a,b∈Ma,b\in M mit a≤ba\leq b stets: inf⁡{a,b}=min⁡{a,b}=a\inf \{ a,b\}=\min \{ a,b\}=a und sup⁡{a,b}=max⁡{a,b}=b\sup \{ a,b\}=\max \{ a,b\}=b.

Teilbarkeit

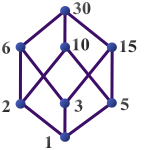
OrdT30.png
Die natürlichen Zahlen mit der Teilbarkeit als Ordnung sind Infimum und Supremum zweier Zahlen definiert. Dabei entspricht das Infimum dem größten gemeinsamen Teiler und das Supremum dem kleinsten gemeinsamen Vielfachen.
inf⁡(10;15)=ggT⁡(10;15)=5\inf( 10;15)=\ggT(10;15)=5
sup⁡(10;15)=kgV⁡(10;15)=30\sup( 10;15)=\kgV(10;15)=30

Beispiel 160H (Mengensysteme)

Sei P(M)\Pow(M) die Potenzmenge von MM. Diese bildet bzgl. der Inklusion ⊆\subseteq eine teilweise geordnete Menge. Für je zwei Mengen A,B∈P(M)A,B\in \Pow(M) existieren Infimum und Supremum und es gilt:
inf⁡{A,B}=A∩B\inf\{ A,B\}=A\cap B und sup⁡{A,B}=A∪B\sup\{ A,B\}=A\cup B,
das Infimum entspricht also dem Durchschnitt und das Supremum der Vereinigung.
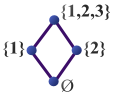
TM3Nv.png
Für beliebige Mengensysteme M⊆P(M)\sb M\subseteq \Pow(M) kann man mit der Inklusion eine Ordnung definieren. Infimum und Supremum zweier Mengen A,B∈MA,B\in \sb M müssen dann nicht notwendigerweise existieren, und wenn sie existieren nicht mit dem Durchschnitt und der Vereinigung übereinstimmen (siehe nebenstehendes Hassediagramm).

Ich stimme mit der Mathematik nicht überein. Ich meine, daß die Summe von Nullen eine gefährliche Zahl ist.

Stanislaw Jerzy Lec

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Teilweise geordnete Mengen