Universalität der Mengensysteme

In Beispiel 160H wurde gezeigt, dass beliebige Mengensysteme mit der Inklusion als Ordnung teilweise geordnete Mengen bilden. Diese Mengensysteme kann man sogar als die universellen Vertreter teilweise geordneter Mengen ansehen, denn der nachfolgende Satz klärt, dass sich für jede teilweise geordnete Menge ein Mengensystem konstruieren lässt, zu dem diese ordnungsisomorph ist.

Satz 160I (Zu teilweise geordneten Mengen ordnungsisomorphe Mengensysteme)

Sei (M,≤)(M,\leq) eine teilweise geordnete Menge. Dann gibt es ein Mengensystem M⊆P(M)\sb M\subseteq \Pow(M) und einen dazugehörigen kanonischen Ordnungsisomorphismus f:M→Mf: M\rightarrow \sb M. Dieser bildet ein m∈Mm\in M auf die Minorante Mi⁡(m)∈P(M)\Mi(m)\in\Pow(M) von mm ab. Das Mengensystem M\sb M besteht damit aus allen Minoranten von Elementen aus MM.

Beispiel

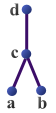
Ms4.png
Für das nebenstehende Hassediagramm finden wir die kanonische Abbildung: a↦Mi⁡(a)={a}a\mapto \Mi(a)=\{a\}; b↦Mi⁡(b)={b}b\mapto \Mi(b)=\{b\}; c↦Mi⁡(c)={a,b,c}c\mapto \Mi(c)=\{a,b,c\}; d↦Mi⁡(d)={a,b,c,d}d\mapto \Mi(d)=\{a,b,c,d\}.

Beweis

ff ist nach Konstruktion sicher surjektiv.
Seien a,b∈Ma,b\in M; dann ist f(a)=Mi⁡(a)f(a)=\Mi(a) und f(b)=Mi⁡(b)f(b)=\Mi(b). Wenn nun Mi⁡(a)=Mi⁡(b)\Mi(a)=\Mi(b) ist, gilt sowohl a≤ba\leq b als auch b≤ab\leq a, und damit a=ba=b, also ist ff injektiv.
Nach Satz 1601 (iv) ist a≤b  ⟺  Mi⁡(a)⊆Mi⁡(b)a\leq b\iff \Mi(a)\subseteq\Mi(b), damit sind ff und f −1f^{\, \me} isoton.
Damit ist gezeigt, dass ff ein Ordnungsisomorphismus ist. □\qed
 
 

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Teilweise geordnete Mengen