Lineare Optimierung

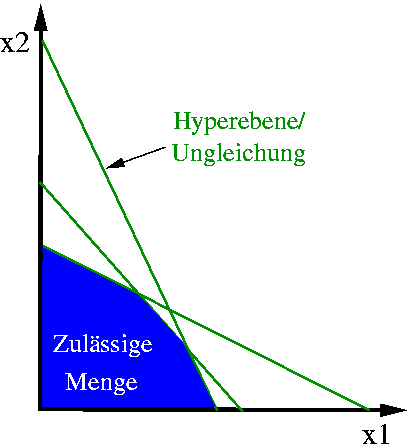
Linopt-feasible-region.png
Bei linearen Optimierungsproblemen ist die Menge der zulässigen Punkte (blau) durch lineare Ungleichungen (Hyperebenen, grün) eingeschränkt.
Die Lineare Optimierung oder auch Lineare Programmierung ist eines der Hauptverfahren des Operations Research und beschäftigt sich mit der Optimierung linearer Zielfunktionen über einer Menge, die durch lineare Gleichungen und Ungleichungen eingeschränkt ist. Häufig lassen sich lineare Programme (LPs) zur Lösung von Problemen einsetzen, für die keine speziell entwickelten Lösungsverfahren bekannt sind, beispielsweise bei der Planung von Verkehrs- oder Telekommunikationsnetzen oder in der Produktionsplanung. Die lineare Optimierung ist ein Spezialfall der konvexen Optimierung und Grundlage mehrerer Lösungsverfahren in der ganzzahligen linearen und der nichtlinearen Optimierung. Viele Eigenschaften linearer Programme lassen sich auch als Eigenschaften von Polyedern interpretieren und auf diese Art geometrisch motivieren und beweisen.
Der Begriff "Programmierung" ist eher im Sinne von "Planung" zu verstehen als im Sinne der Erstellung eines Computerprogramms. Er wurde schon Mitte der 1940er Jahre von George Dantzig, einem der Begründer der Linearen Optimierung, geprägt, bevor Computer zur Lösung linearer Optimierungsprobleme eingesetzt wurden.
Aus komplexitätstheoretischer Sicht ist die lineare Optimierung ein einfaches Problem, da es sich beispielsweise mit einigen Innere-Punkte-Verfahren in polynomialer Zeit lösen lässt. In der Praxis hat sich allerdings das Simplex-Verfahren als einer der schnellsten Algorithmen herausgestellt, obwohl er im schlechtesten Fall exponentielle Laufzeit besitzt. Neben dem eigentlichen Problem löst es immer auch das sogenannte duale Problem mit, was unter anderem in mehreren Verfahren zur Lösung ganzzahliger linearer Programme ausgenutzt wird.

Geschichte

Die lineare Optimierung wurde erstmals 1939 von dem sowjetischen Mathematiker Leonid Witaljewitsch Kantorowitsch in seinem Buch "Mathematische Methoden in der Organisation und Planung der Produktion" behandelt. Kurz danach veröffentlichte der Amerikaner Frank L. Hitchcock eine Arbeit zu einem Transportproblem. Damals erkannte man noch nicht die Bedeutung dieser Arbeiten. Unter anderem für seinen Beitrag zur linearen Optimierung bekam Kantorowitsch aber 1975 den Nobelpreis für Wirtschaftswissenschaften.
Mitte der 1940er Jahre erkannte George Dantzig, dass sich viele praktische Beschränkungen durch lineare Ungleichungen beschreiben ließen, und ersetzte erstmals die bis dahin vorherrschenden Faustregeln zur Lösung von Planungsproblemen durch eine (lineare) Zielfunktion. Insbesondere etablierte er damit eine klare Trennung zwischen dem Ziel der Optimierung und den Mitteln zur Lösung des Planungsproblems.
Den Durchbruch für die lineare Optimierung schaffte Dantzig 1947, als er eine Arbeit über das Simplex-Verfahren veröffentlichte, das heute eines der meistgenutzten Verfahren zur Lösung linearer Programme ist. Interesse an dieser Arbeit zeigten zunächst die amerikanischen Militärs, speziell die US Air Force, die militärische Einsätze optimieren wollten. In den Folgejahren entwickelten Dantzig, John von Neumann, Oscar Morgenstern, Tjalling Koopmans und andere das Verfahren und die zugehörige Theorie weiter und stellten Zusammenhänge zur Spieltheorie her. Mit dem Aufkommen von Computern Mitte der 1950er Jahre konnte man auch größere Probleme lösen. Etwa ab 1950 entdeckte die Wirtschaft, insbesondere Ölraffinerien, die Anwendungsmöglichkeiten der linearen Optimierung. Ab den 1970er Jahren profitierte der Simplex-Algorithmus von algorithmischen Fortschritten der numerischen linearen Algebra. Insbesondere die Entwicklung numerisch stabiler LR-Zerlegungen zur Lösung großer linearer Gleichungssysteme trugen maßgeblich zum Erfolg und der Verbreitung des Simplex-Verfahrens bei.
Im Jahre 1979 veröffentlichte Leonid Khachiyan die Ellipsoidmethode, mit der lineare Programme erstmals - zumindest theoretisch - in polynomialer Zeit gelöst werden konnten. Mitte der 1980er Jahre begannen Narendra Karmarkar und andere mit der Entwicklung von Innere-Punkte-Verfahren zur Lösung linearer Programme. Diese Algorithmen, die als erste polynomiale Lösungsmethoden auch das Potential zum praktischen Einsatz hatten, wurden innerhalb des nachfolgenden Jahrzehnts noch wesentlich verbessert. Parallel dazu wuchs die Bedeutung des Simplex-Verfahrens zur Lösungen von Unterproblemen in der ganzzahligen linearen Optimierung. Anfang der 1990er Jahre wurden hier noch einmal große Fortschritte durch die Entwicklung neuer Pivotstrategien für den dualen Simplex-Algorithmus erzielt, insbesondere durch das dual steepest edge pricing von John Forrest und Donald Goldfarb.
Sowohl das Simplex-Verfahren als auch verschiedene Innere-Punkte-Verfahren sind nach wie vor Gegenstand aktueller Forschung. Die lineare Optimierung wird heute in sehr vielen Bereichen zur Lösung praktischer Probleme eingesetzt. Unter der in praktischen Anwendungen fast immer erfüllten Voraussetzung, dass die auftretenden LP-Matrizen dünnbesetzt sind (also nur wenige Nicht-Null-Einträge besitzen), können heute lineare Programme mit mehreren Hunderttausend Variablen oder Ungleichungen innerhalb weniger Minuten bis Stunden optimal gelöst werden. Die tatsächliche Lösungszeit hängt dabei neben dem verwendeten Lösungsverfahren auch stark von der Anzahl und Anordnung der Nicht-Null-Einträge in der beteiligten Matrix und von der Wahl der Startlösung ab.

Problemdefinition

Mathematische Formulierung

Bei einem linearen Programm (LP) sind eine Matrix A∈Rm,nA\in\R^{m,n} und zwei Vektoren b∈Rmb\in\R^m und c∈Rnc\in\R^n gegeben. Eine zulässige Lösung ist ein Vektor x∈Rnx \in \R^n mit nichtnegativen Einträgen, der die linearen Bedingungen
a11x1+…+a1nxn≤b1a21x1+…+a2nxn≤b2⋮⋮⋮⋮am1x1+…+amnxn≤bm \begin{matrix} a_{11} x_1 &+ \ldots &+ a_{1n} x_n &\leq b_1 \\ a_{21} x_1 &+ \ldots &+ a_{2n} x_n &\leq b_2 \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} x_1 &+ \ldots &+ a_{mn} x_n &\leq b_m \end{matrix}
erfüllt. Ziel ist es, unter allen zulässigen Vektoren xx einen zu finden, der das Skalarprodukt
cTx=c1x1+…+cnxnc^T x = c_1 x_1 + \ldots + c_n x_n
maximiert. Dieses Optimierungsproblem in der sogenannten Standardform wird oft abkürzend als
max⁡{cTx  ∣  Ax≤b,x≥0}\max \{ c^T x \;|\; A x \leq b, x \geq 0 \}
geschrieben, wobei die Bedingungen Ax≤bA x \le b und x≥0x \geq 0 komponentenweise zu verstehen sind.
Darüber hinaus gibt es noch weitere äquivalente Formulierungen, die sich durch einfache Operationen in diese Standardform bringen lassen:
  • Minimierungsproblem statt Maximierungsproblem: Multiplikation des Zielfunktionsvektors cc mit (-1)
  • Größer-gleich- statt Kleiner-gleich-Bedingungen: Multiplikation der entsprechenden Ungleichungen mit (-1)
  • Gleichheitsbedingungen statt Ungleichheitsbedingungen: Ersetzung von aix=bia_i x = b_i durch aix≤bia_i x \leq b_i und −aix≤−bi - a_i x \leq - b_i
  • Variablen ohne Nichtnegativitätsbedingung: Ersetzung von xx durch x′−x′′x' - x'' mit x′,x′′≥0x', x'' \ge 0
Die lineare Optimierung behandelt nur Probleme, bei denen die Variablen beliebige reelle Zahlen annehmen dürfen. Ein (gemischt-)ganzzahliges lineares Programm, bei dem einige Variablen nur ganzzahlige Werte annehmen dürfen, ist kein Spezialfall. Solche Optimierungsprobleme sind im allgemeinen NP-äquivalent, d. h. vermutlich nicht effizient lösbar. Dieser Fall wird von der ganzzahligen linearen Optimierung behandelt.

Geometrische Interpretation

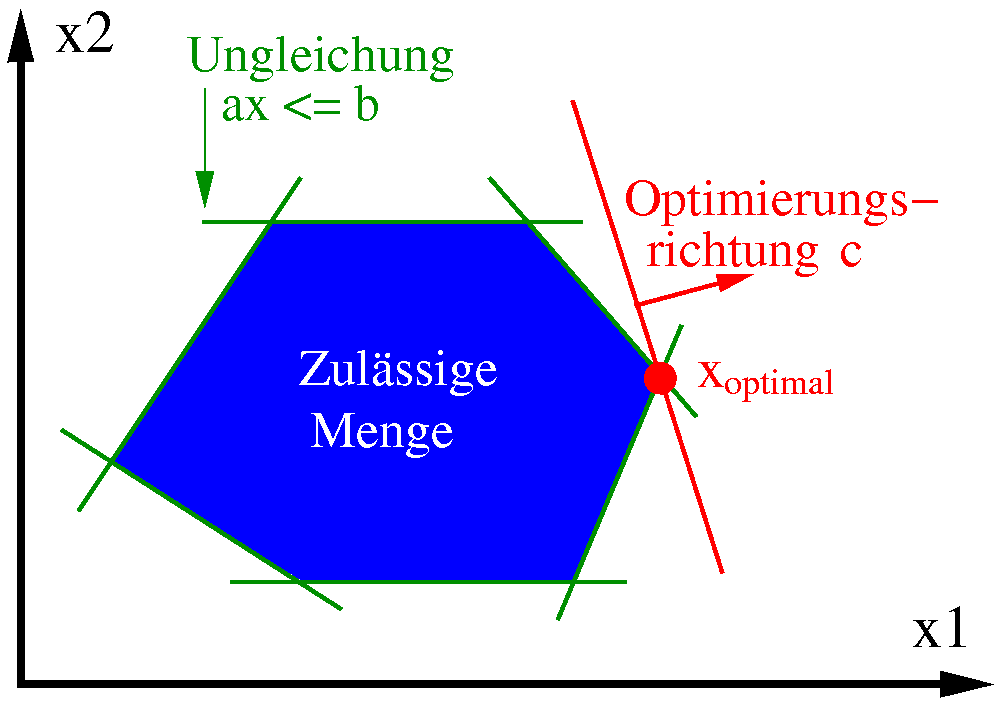
Linopt-feasible-region2.png
Zulässige Menge (blau) eines LPs in Standardform mit einschränkenden Ungleichungen (grün), Zielfunktion (rote Linie) und einer optimalen Lösung (roter Punkt).
Ein lineares Programm lässt sich geometrisch interpretieren. Wenn aix≤bia_i x \leq b_i die i. Zeile eines linearen Programms in Standardform ist, dann beschreibt die Menge {x  ∣  aix=bi}\{ x \; | \; a_i x = b_i \} aller Punkte xx, die die zugehörige lineare Gleichung aix=bia_i x = b_i erfüllen, eine Hyperebene im nn-dimensionalen Raum. Die Menge der Punkte, die die lineare Ungleichung aix≤bia_i x \leq b_i erfüllen, besteht dann aus allen Punkten auf der einen Seite der Hyperebene (inklusive der Hyperebene selbst), bildet also einen Halbraum. Jede Zeile aix≤bia_i x \leq b_i teilt daher den nn-dimensionalen Raum in zwei Hälften, wobei die Punkte in der einen Hälfte zulässig sind und in der anderen nicht. Die Menge
P:={x  ∣  Ax≤b,  x≥0}={x  ∣  aix≤bi,  i=1,…,m,  x≥0}P := \{ x \; | \; Ax \leq b, \; x \geq 0 \} = \{ x \; | \; a_i x \leq b_i, \; i = 1,\ldots,m, \; x \geq 0 \}
der Punkte, die alle Ungleichungen des LPs erfüllen, ist genau der Schnitt dieser Halbräume, also die Menge aller Punkte, die für jede Ungleichung in der jeweiligen zulässigen Hälfte des Raumes liegen. Diese Lösungsmenge PP des linearen Programms bildet ein konvexes Polyeder, also ein nn-dimensionales Vieleck, in dem die Verbindungslinie zwischen zwei beliebigen Punkten von PP vollständig in PP enthalten ist. Ziel der Optimierung ist es, unter allen Punkten des Polyeders einen zu finden, der die lineare Funktion c: x→cTxc:\,x \to c^T x maximiert. Geometrisch entspricht dies der Verschiebung der Hyperebene {x  ∣  cTx=0}\{ x \; | \; c^T x = 0 \} in Richtung des Vektors cc, bis die verschobene Hyperebene das Polyeder gerade noch berührt. Die Menge aller Berührungspunkte ist genau die Menge der Optimallösungen des linearen Programms.
Im nebenstehenden Bild ist diese Anordnung für den Fall von nur zwei Variablen dargestellt. Eine Hyperebene im zweidimensionalen Raum ist eine Gerade, im Bild grün dargestellt. Jede dieser Geraden teilt den Raum in eine zulässige und eine unzulässige Hälfte. Die Menge der Punkte, die auf der zulässigen Seite jeder Geraden liegen, bilden das blau dargestellte Polyeder (Vieleck). Die rote Gerade stellt die Zielfunktion dar. Ziel ist es, sie so weit wie möglich in Richtung des roten Vektors cc zu verschieben, ohne das Polyeder zu verlassen. Im nebenstehenden Bild ist der rote Berührungspunkt der Zielfunktionsgeraden mit dem Polyeder die einzige Optimallösung.

Beispiel aus der Produktionsplanung

Eine Firma stellt zwei verschiedene Produkte her, für deren Fertigung drei Maschinen A, B, C zur Verfügung stehen. Diese Maschinen haben eine maximale monatliche Laufzeit (Kapazität) von 170 Stunden (A), 150 Stunden (B) bzw. 180 Stunden (C). Eine Mengeneinheit (ME) von Produkt 1 liefert einen Deckungsbeitrag von 300 Euro, eine ME von Produkt 2 dagegen 500 Euro. Fertigt man eine ME von Produkt 1, dann benötigt man dafür eine Stunde die Maschine A und eine Stunde die Maschine B. Eine Einheit von Produkt 2 belegt zwei Stunden lang Maschine A, eine Stunde Maschine B und drei Stunden Maschine C. Ziel ist es, Produktionsmengen zu bestimmen, die den Deckungsbeitrag der Firma zu maximieren, ohne die Maschinenkapazitäten zu überschreiten. Fixkosten können in dem Optimierungsproblem ignoriert und anschließend dazuaddiert werden, da sie per Definition unabhängig von den zu bestimmenden Produktionsmengen sind.

Mathematische Modellierung

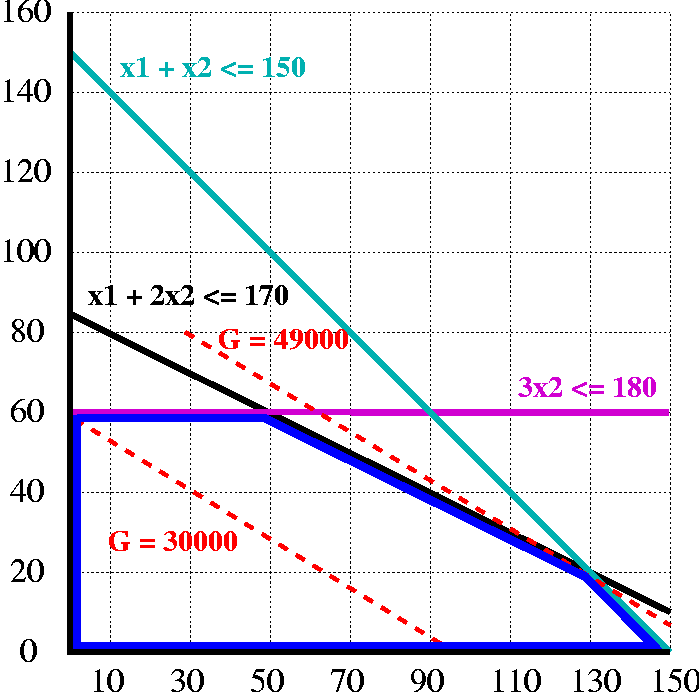
Linear_programming_polytope.png
Veranschaulichung des Beispiels (Erklärung siehe Text)
Angenommen, der Betrieb fertigt pro Monat x1x_{1} ME von Produkt 1 und x2x_{2} ME von Produkt 2. Dann beträgt der Gesamtdeckungsbeitrag
G(x1,x2)=300x1+500x2G(x_1,x_2) = 300 x_1 + 500 x_2
Diesen Wert möchte die Firma maximieren. Da die Maschinenkapazitäten eingehalten werden müssen, ergeben sich die Nebenbedingungen:
x1+2x2≤170(Maschine A)x1+x2≤150(Maschine B)3x2≤180(Maschine C) \begin{matrix} x_1 + &2x_2 &\leq 170 & \text{(Maschine A)}\\ x_1 + & x_2 &\leq 150 & \text{(Maschine B)}\\ &3x_2 &\leq 180 & \text{(Maschine C)} \end{matrix}
Da außerdem keine negativen Produktionsmengen möglich sind, muss x1,  x2≥0x_1, \; x_2 \geq 0 gelten (Nichtnegativitätsbedingung).

Geometrische Interpretation als Polyeder

Im nebenstehenden Bild sind die Ungleichungen aus dem obigen Beispiel als hellblaue, schwarze und violette Beschränkungen eingezeichnet. Zusammen definieren sie das (blau umrandete) Polyeder der zulässigen Punkte. Die rotgestrichelten Linien stellen Iso-Gewinnfunktionen dar, d. h. alle Punkte auf einer solchen Linie haben denselben Zielfunktionswert. Da die Firma möglichst viel produzieren will, ist das Ziel der Optimierung, solch eine rot gestrichelte Linie soweit nach rechts oben zu schieben, so dass sie gerade noch das Polyeder berührt. Alle Berührungspunkte sind dann optimal. In diesem Fall ist der Punkt (130,20) die eindeutige optimale Ecke, und der optimale Zielfunktionswert beträgt 49.000 Euro.
Im allgemeinen ist die Optimallösung eines linearen Optimierungsproblems allerdings weder eindeutig noch ganzzahlig. Wenn beispielsweise beide Produkte den gleichen Deckungsbeitrag hätten, wären die roten Iso-Gewinnfunktionen parallel zur Ungleichung x1+x2≤150x_1 + x_2 \leq 150. In diesem Fall wäre jeder Punkt auf der Strecke zwischen (130,20) und (150,0) optimal, es gäbe also unendliche viele Optimallösungen.

Anwendungen

Die lineare Optimierung hat viele Anwendungen in der Praxis, von denen hier einige beispielhaft vorgestellt werden sollen.

Produktionsplanung

Wie in dem obigen Beispiel kann ein Unternehmen eine Reihe von Produkten mit bekanntem Deckungsbeitrag herstellen. Die Herstellung einer Einheit jedes dieser Produkte benötigt eine bekannte Menge an beschränkten Ressourcen (Produktionskapazität, Rohmaterialien, etc). Die Aufgabe ist die Erstellung eines Produktionsplans, d. h. die Festlegung, wieviel von jedem Produkt produziert werden soll, so dass der Profit der Firma maximiert wird, ohne die Ressourcenbeschränkungen zu verletzen.

Mischungsprobleme

Eine ähnliche Anwendung sind Mischungsprobleme, bei denen es darum geht, Zutaten zu einem Endprodukt zusammenzustellen, wobei die Menge der jeweiligen Zutaten innerhalb eines bestimmten Bereichs variiert werden kann. Ein Beispiel hierfür ist das 1947 von George Dantzig untersuchte Diät-Problem: Gegeben sind eine Reihe von Rohmaterialien (z. B. Hafer, Schweinefleisch, Sonnenblumenöl, etc.) zusammen mit ihrem Gehalt an bestimmten Nährwerten (z. B. Eiweiß, Fett, Vitamin A, etc.) und ihrem Preis pro Kilogramm. Die Aufgabe besteht darin, eines oder mehrere Endprodukte mit minimalen Kosten aus den Rohmaterialien zu mischen, unter der Nebenbedingung, dass bestimmte Mindest- und Höchstgrenzen für die einzelnen Nährwerte eingehalten werden. Auch bei Schmelzvorgängen treten solche Mischungsprobleme auf, wie z. B. in der Stahlherstellung.

Routing in Telekommunikations- oder Verkehrsnetzen

Ein klassisches Anwendungsgebiet der linearen Optimierung ist die Bestimmung eines Routings für Verkehrsanforderungen in Telekommunikations- oder Verkehrsnetzen, oft in Verbindung mit Kapazitätsplanung. Dabei müssen Verkehrsflüsse so durch ein Netz geroutet werden, dass alle Verkehrsanforderungen erfüllt werden, ohne die Kapazitätsbedingungen zu verletzen. Diese sogenannten Mehrgüterflüsse (engl. multicommodity flow) sind auch ein Beispiel für ein Problem, das mit linearer Optimierung gut lösbar ist, für das aber im allgemeinen Fall kein exakter Algorithmus bekannt ist, der nicht auf LP-Theorie basiert.

Spieltheorie

Innerhalb der mathematischen Spieltheorie kann die lineare Optimierung dazu verwendet werden, optimale Strategien in Zwei-Personen-Nullsummenspielen zu berechnen. Dabei wird für jeden Spieler eine Wahrscheinlichkeitsverteilung berechnet, bei der es sich um ein zufälliges Mischungsverhältnis seiner Strategien handelt. "Würfelt" ein Spieler seine Strategie gemäß dieser Wahrscheinlichkeitsverteilung zufällig aus, ist ihm die bestmögliche Gewinnerwartung sicher, die er haben kann, wenn er seine Strategie unabhängig von der seines Gegners wählt.

Nichtlineare und ganzzahlige Optimierung

Viele Anwendungsprobleme lassen sich mit kontinuierlichen Variablen nicht sinnvoll modellieren, sondern erfordern die Ganzzahligkeit einiger Variablen. Beispielsweise können keine 3,7 Flugzeuge gekauft werden, sondern nur eine ganze Anzahl, und ein Bus kann nur ganz oder gar nicht fahren, aber nicht zu zwei Dritteln. Bei der Verwendung von Branch-and-Cut zur Lösung eines solchen ganzzahligen linearen Optimierungsproblems müssen sehr viele ähnliche lineare Programme hintereinander als Unterproblem gelöst werden. Auch zur Lösung nichtlinearer Optimierungsprobleme gibt es Algorithmen, in denen lineare Programme als Unterproblem gelöst werden müssen (z. B. Sequential Linear Programming).

Lösbarkeit aus theoretischer Sicht

Ein lineares Programm hat nicht immer eine Optimallösung. Drei Fälle sind zu unterscheiden:
  1. Das LP ist unzulässig, weil sich Ungleichungen widersprechen (z. B. x≤1x \leq 1 und x≥2x \geq 2). In diesem Fall gibt es keine Lösung, die alle Ungleichungen erfüllt, d. h. das zugehörige Polyeder ist die leere Menge.
  2. Das LP ist unbeschränkt, d. h. es gibt unendlich viele zulässige Lösungen mit beliebig hohen Zielfunktionswerten (z. B. max⁡{x  ∣  x≥0}\max \{ x \;|\; x \geq 0\}).
  3. Das LP besitzt mindestens eine Optimallösung. Dies ist unter anderem dann gegeben, wenn das zugehörige Polyeder beschränkt, also ein (nichtleeres) Polytop ist.
Die Menge der Optimallösungen bildet eine Seitenfläche (Ecke, Kante,...) des Polyeders, so dass es entweder keine, genau eine oder unendlich viele Optimallösungen gibt. Letzteres bedeutet anschaulich, dass die Zielfunktion parallel zu einer beschränkenden Hyperebene liegt. Wenn das LP lösbar und beschränkt ist, gibt es auch immer eine optimale Ecke, also einen optimalen Punkt, der nicht aus anderen Punkten des Polyeders konvex kombiniert werden kann. Diese Eigenschaft macht sich u. a. das Simplex-Verfahren zunutze.

Komplexität und Lösungsverfahren

Das Finden einer Optimallösung bzw. die Feststellung, dass ein LP keine Lösung besitzt, ist mit Hilfe von Innere-Punkte-Verfahren oder der Ellipsoidmethode in Polynomialzeit möglich, so dass die Lineare Optimierung aus Sicht der Komplexitätstheorie ein leicht lösbares Problem ist. Aus praktischer Sicht ist jedoch oft das Simplex-Verfahren schneller, obwohl es theoretisch exponentielle Laufzeit besitzt. Es ist bis heute unbekannt, ob es einen streng polynomialen Algorithmus zur Lösung allgemeiner linearer Programme gibt, d. h. einen Algorithmus, dessen Laufzeit nicht von der Größe der auftretenden Zahlen abhängt.

Simplex-Verfahren

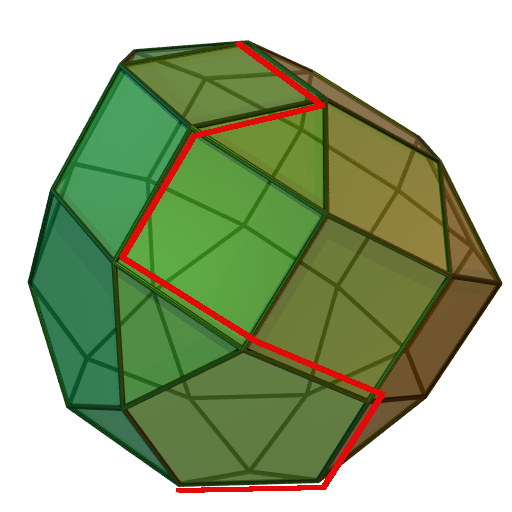
Simplex-method-3-dimensions.png
siehe Hauptartikel: Simplex-Verfahren
Das Simplex-Verfahren, das im Jahre 1947 von George Dantzig entwickelt und seitdem wesentlich verbessert wurde, ist der wichtigste Algorithmus zur Lösung linearer Programme in der Praxis. Die Grundidee besteht darin, von einer Ecke des Polyeders zu einer benachbarten Ecke mit besserem Zielfunktionswert zu laufen, bis dies nicht mehr möglich ist. Da es sich bei der linearen Optimierung um ein konvexes Optimierungsproblem handelt, ist die damit erreichte lokal optimale Ecke auch global optimal. Das Verfahren ist im nebenstehenden Bild illustriert: Ziel ist es, einen möglichst weit oben liegenden Punkt des Polyeders zu finden. In roter Farbe ist ein möglicher Pfad des Simplex-Verfahrens entlang der Ecken des Polyeders dargestellt, wobei sich der Zielfunktionswert mit jedem Schritt verbessert.
Aus komplexitätstheoretischer Sicht benötigt der Simplex-Algorithmus im schlechtesten Fall exponentielle Laufzeit. Für jede Variante des Algorithmus konnte bisher ein Beispiel konstruiert werden, bei dem der Algorithmus alle Ecken des Polyeders abläuft, meist basierend auf dem Klee-Minty-Würfel. Aus praktischer Sicht sind solche Fälle allerdings sehr selten. Bei sogenannten degenerierten (man spricht auch von entarteten) linearen Programmen, bei denen eine Ecke durch mehr Ungleichungen definiert wird als unbedingt nötig (beispielsweise durch drei Ungleichungen im zweidimensionalen Raum), kann es allerdings passieren, dass der Algorithmus immer wieder dieselbe Ecke betrachtet, anstatt zur nächsten Ecke zu wechseln. Dieses Problem tritt bei praktischen Planungsproblemen häufig auf und kann dazu führen, dass der Algorithmus nicht terminiert oder der Zielfunktionswert sich über viele Iterationen hinweg nicht verbessert. Gute Simplex-Implementierungen entdecken solche Fälle und behandeln sie beispielsweise durch eine leichte Perturbation (absichtliche numerische Störung) des Problems, die später wieder rückgängig gemacht wird.
Unter der Voraussetzung, dass die Matrix AA dünnbesetzt ist (d. h. nur wenige Koeffizienten ungleich Null enthält), was in der Praxis fast immer der Fall ist, können mit dem Simplex-Verfahren heute sehr große LPs in annehmbarer Zeit optimal gelöst werden. Ein großer Vorteil des Simplex-Verfahrens besteht darin, dass es nach dem Hinzufügen einer Ungleichung oder Variable im LP oder nach einer leichten Änderung der Koeffizienten einen "Warmstart" von einer vorher bereits erreichten Ecke aus durchführen kann, so dass nur wenige Iterationen zum erneuten Finden einer Optimallösung notwendig sind. Dies ist insbesondere im Zusammenhang mit Schnittebenenverfahren oder Branch-and-Cut zur Lösung ganzzahliger linearer Programme von großer Bedeutung, wo sehr viele ähnliche LPs in Serie gelöst werden müssen.

Innere-Punkte-Verfahren

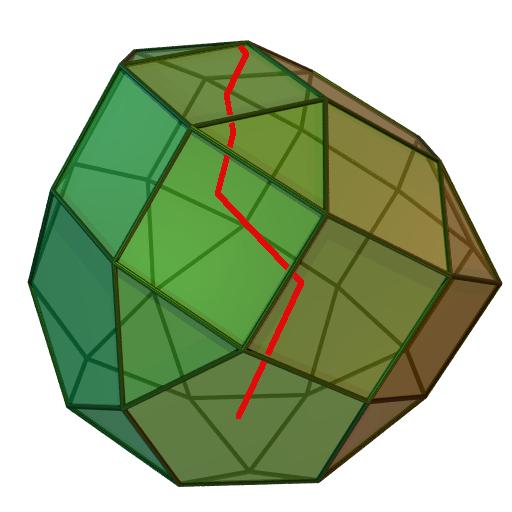
Interior-point-method-three-dimensions.png
siehe Hauptartikel: Innere-Punkte-Verfahren
Innere-Punkte-Verfahren, auch Barrier-Verfahren genannt, nähern sich einer optimalen Ecke durch das Innere des Polyeders (siehe Bild). Der erste solche Algorithmus wurde 1984 von Narendra Karmarkar beschrieben. Seine Bedeutung lag vor allem darin, dass er der erste polynomiale Algorithmus zum Lösen linearer Programme war, der das Potential hatte, auch praktisch einsetzbar zu sein. Die entscheidenden Durchbrüche, die Innere-Punkte-Verfahren konkurrenzfähig zum Simplex-Algorithmus machten, wurden aber erst in den 1990er Jahren erzielt. Ein Vorteil dieser Verfahren ist, dass sie, im Gegensatz zum Simplex-Verfahren, in leichter Abwandlung auch zum Lösen quadratischer oder bestimmter nichtlinearer Programme eingesetzt werden können. Des weiteren sind sie für große, dünnbesetzte Probleme häufig dem Simplex-Verfahren überlegen. Ein Nachteil ist, dass sie sich nach dem Hinzufügen einer Nebenbedingung oder Variablen im LP bei weitem nicht so effizient "warmstarten" lassen wie das Simplex-Verfahren.

Ellipsoidmethode

Ellipsoid-method.png
siehe Hauptartikel: Ellipsoidmethode
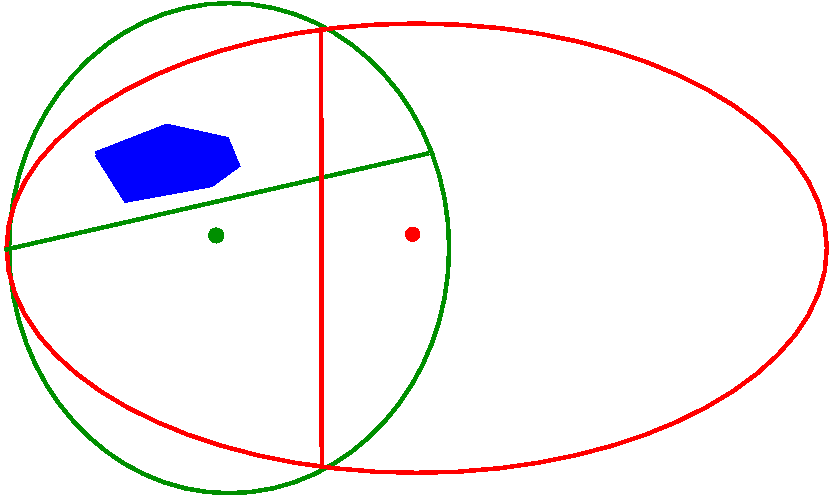
Die Ellipsoidmethode wurde ursprünglich in den Jahren 1976 und 1977 von David Yudin and Arkadi Nemirovski und unabhängig davon von Naum Shor zur Lösung konvexer Optimierungsprobleme entwickelt. Im Jahre 1979 modifizierte der russische Mathematiker Leonid Khachiyan das Verfahren und entwickelte damit den ersten polynomialen Algorithmus zur Lösung linearer Programme. Für praktische Zwecke ist er allerdings nicht geeignet. Die Ellipsoidmethode dient dazu, einen beliebigen Punkt in einem volldimensionalen Polyeder zu finden oder festzustellen, dass das Polyeder leer ist. Da man zeigen kann, dass die Lösung eines LPs äquivalent ist zum Finden eines zulässigen Punktes in einem geeignet definierten Hilfspolyeder, lässt sich mit Hilfe der Ellipsoidmethode (theoretisch) auch ein LP lösen.
Die Grundidee des Verfahrens besteht darin, ein Ellipsoid (im Bild rot) zu definieren, das alle Ecken des Polyeders (blau) enthält. Anschließend wird festgestellt, ob der Mittelpunkt dieses Ellipsoids im Polyeder enthalten ist. Falls ja, hat man einen Punkt im Polyeder gefunden und kann aufhören. Andernfalls kann man das Halbellipsoid bestimmen, in dem das Polyeder enthalten sein muss, und ein neues, kleineres Ellipsoid um das Polyeder legen (im Bild grün). Nach einer Anzahl von Schritten, die polynomial von der Kodierungslänge des LPs abhängt, hat man entweder einen Punkt im Polyeder gefunden oder weiß, dass das Polyeder leer ist, weil es sonst größer sein müsste als das aktuelle Ellipsoid.

Weitere Methoden

Für einige Klassen von linearen Programmen gibt es spezielle Algorithmen, die theoretisch oder praktisch schneller laufen als z. B. der Simplexalgorithmus. Ein Beispiel hierfür ist die Ungarische Methode, die auf Zuordnungsprobleme angewandt werden kann. Lineare Programme mit zwei Variablen lassen sich auch näherungsweise zeichnerisch lösen (siehe obiges Beispiel). Diese Methode hat aber hauptsächlich didaktischen Wert, da in der Praxis auftretende LPs leicht mehrere Hunderttausende Variablen besitzen können.

Dualität

Jedem linearen Programm (dem primalen Problem) ist ein anderes lineares Programm zugeordnet: das duale Problem. Zwischen dem primalen und seinem dualen Problem gibt es enge Zusammenhänge, die sowohl beim Beweis von Sätzen der linearen Optimierung als auch bei der praktischen Lösung linearer oder ganzzahlig-linearer Programme ausgenutzt werden können. Einige dieser Zusammenhänge sind Spezialfälle der entsprechenden Sätze aus der konvexen Optimierung.
Einem primalen LP in Standardform
max⁡  {cTx : Ax≤b,  x≥0}\max \; \{ c^T x \,:\, Ax \le b,\; x \ge 0\}
ist das duale LP
min⁡  {bTy : ATy≥c,  y≥0}\min \; \{ b^T y \,:\, A^T y \ge c,\; y \ge 0\}
zugeordnet, bei dem die Zeilen und Spalten gegenüber dem Ausgangsproblem vertauscht sind. Jeder Ungleichung des primalen Problems ist dabei eine sogenannte Dualvariable yiy_i zugeordnet, und jeder Variable xjx_j des primalen Problems entspricht eine duale Ungleichung. Das duale Problem des dualen Problems ist wieder das Ursprungsproblem.
Die Zusammenhänge zwischen dem primalen und dualen Problem werden durch die sogenannten Dualitätssätze beschrieben, die alle auf Farkas' Lemma basieren. Nach dem schwachen Dualitätssatz der linearen Optimierung gilt für alle zulässigen Lösungen xx und yy des primalen bzw. dualen Problems
cTx≤bTyc^Tx \le b^T y,
d. h. der Wert jeder dualen Lösung ist mindestens so hoch wie der Wert jeder primalen Lösung.
Der starke Dualitätssatz verschärft diese Aussage: wenn eines der beiden LPs eine beschränkte Optimallösung besitzt, dann auch das andere, und die optimalen Zielfunktionswerte sind in diesem Fall gleich. Für alle optimalen Lösungen x∗,y∗x^*, y^* des primalen und dualen Problems gilt also cTx∗=bTy∗c^Tx^* = b^Ty^*.
Man kann zeigen, dass folgende Zusammenhänge gelten:
  • Das duale Problem hat genau dann eine beschränkte Optimallösung, wenn das primale Problem eine beschränkte Optimallösung besitzt.
  • Wenn das primale Problem keine zulässige Lösung hat, ist das duale Problem unbeschränkt oder hat auch keine zulässige Lösung.
  • Wenn das primale Problem unbeschränkt ist, hat das duale Problem keine zulässige Lösung.
Diese und weitere Sätze bilden die Grundlage für alle Verfahren, die mit primalen und dualen Schranken für den Wert einer Optimallösung arbeiten, wie beispielsweise Branch-and-Cut und Schnittebenenverfahren.

Literatur

  • Robert Bixby: Solving real-world linear programs: A decade and more of progress. In: Operations Research, Band 50, Nr. 1, 2002, S. 3-15.
  • George B. Dantzig: Lineare Programmierung und Erweiterungen. Springer-Verlag 1966 (Originalausgabe: Linear Programming and Extensions, Princeton University Press, ISBN 0-691-05913-6).
  • Vašek Chvátal: Linear Programming. W. H. Freeman and Company, New York, 1983, ISBN 0-716-71587-2.
  • Alexander Schrijver: Theory of Linear and Integer Programming. John Wiley and Sons. 1998, ISBN 0-471-98232-6.
  • F. L. Hitchcock: The distribution of a product from several sources to numerous localities. In: Journal of Mathematical Physics, Bd. 20, 1941, S. 224-230.
 
 

So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Lineare Optimierung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerik