Simplex-Verfahren

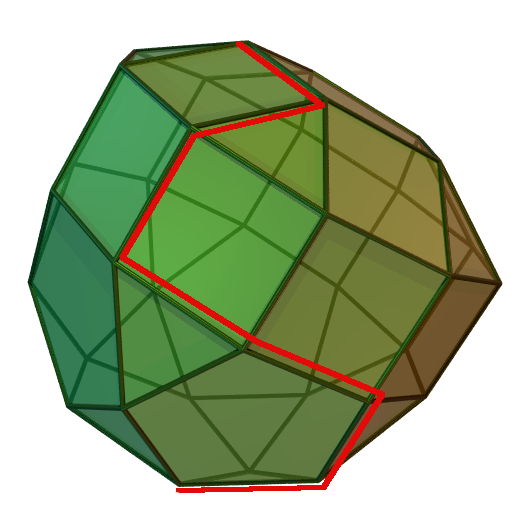
Simplex-method-3-dimensions.png
Das Simplex-Verfahren läuft von einer Ecke eines LP-Polyeders zur nächsten, bis keine Verbesserung mehr möglich ist.
Das Simplex-Verfahren (auch Simplex-Algorithmus) ist im Operations Research ein Optimierungsverfahren zur Lösung linearer Programme (LPs). Es löst ein solches Problem nach endlich vielen Schritten exakt oder stellt dessen Unlösbarkeit oder Unbeschränktheit fest. Die Grundidee des Simplex-Verfahrens wurde 1947 von George Dantzig vorgestellt. Seitdem hat es sich durch zahlreiche Verbesserungen zum wichtigsten Lösungsverfahren der linearen Optimierung in der Praxis entwickelt.
Obwohl bisher für jede Variante des Verfahrens ein Beispiel konstruiert werden konnte, bei dem der Algorithmus exponentielle Laufzeit benötigt, läuft der Simplex-Algorithmus in der Praxis meist schneller als andere Verfahren. Zwar gibt es zur Lösung einzelner linearer Programme auch andere konkurrenzfähige Methoden, z. B. Innere-Punkte-Verfahren. Der große Vorteil des Simplex-Algorithmus liegt jedoch darin, dass er bei leichter Veränderung des Problems - beispielsweise dem Hinzufügen einer zusätzlichen Bedingung - einen "Warmstart" von der letzten verwendeten Lösung durchführen kann und daher meist nur wenige Iterationen zur erneuten Lösung benötigt, während andere Verfahren von vorne beginnen müssen. Darüber hinaus nutzt das Simplex-Verfahren die engen Zusammenhänge zwischen einem linearen Programm und seinem dualen LP aus und löst grundsätzlich beide Probleme gleichzeitig. Beide Eigenschaften sind in der nichtlinearen oder ganzzahligen linearen Optimierung von Bedeutung, wo sehr viele ähnliche LPs in Folge gelöst werden müssen.
Die geometrische Grundidee des Algorithmus besteht darin, von einer beliebigen Ecke des Polyeders, das durch das lineare Programm definiert wird, entlang seiner Kanten zu einer optimalen Ecke zu laufen. Der Name des Verfahrens rührt daher, dass die nichtnegativen Linearkombinationen der Basisspalten in jeder Iteration einen simplizialen Kegel beschreiben. Ein Namensvetter dieses Verfahrens namens Downhill-Simplex-Verfahren basiert ebenfalls auf einem Simplex, ist aber ein iteratives Verfahren zur nichtlinearen Optimierung.

Grundidee des Simplex-Verfahrens

Das Simplex-Verfahren dient zur Lösung linearer Programme der Form
(LP) max⁡{cTx  ∣  Ax=b,  x≥0} \max \{ c^T x \;|\; Ax = b,\; x \geq 0 \},
wobei A∈Rm×nA \in \mathbb{R}^{m \times n} eine Matrix mit reellen Einträgen, c∈Rnc \in \mathbb{R}^n der sogenannte Zielfunktionsvektor und b∈Rmb \in \mathbb{R}^m ein Vektor mit Beschränkungen ist. Ziel ist es, einen Punkt xx zu finden, der das lineare Gleichungssystem erfüllt und einen möglichst hohen Zielfunktionswert G(x)=cTxG(x) = c^T x hat.
Jedes lineare Programm kann durch einfache Umformungen in diese Form gebracht werden. Insbesondere lässt sich ein Minimierungsproblem durch Multiplikation der Zielfunktion mit (-1) in ein Maximierungsproblem verwandeln. Meist wird noch vorausgesetzt, dass alle Einträge von bb nichtnegativ sind, was sich immer durch Multiplikation einzelner Zeilen des Gleichungssystems mit (-1) erreichen lässt.
Geometrisch lässt sich die Menge der zulässigen Lösungen, also die Menge der Punkte mit nichtnegativen Koordinaten, die das lineare Gleichungssystem Ax=bAx = b erfüllen, als konvexes Polyeder (mehrdimensionales Vieleck) PP interpretieren, dessen Dimension durch die Anzahl der Variablen nach oben begrenzt ist. Ziel ist es, einen Punkt xx in PP mit möglichst hohem Zielfunktionswert G(x)G(x) zu finden. Anschaulich entspricht dies der Verschiebung der Hyperebene cTx=0c^Tx = 0 soweit wie möglich in Richtung des Vektors cc, so dass sie gerade noch das Polyeder berührt. Alle Berührungspunkte sind dann optimal.
Für die Menge der zulässigen Lösungen gibt es drei Möglichkeiten:
  1. das LP besitzt keine zulässigen Lösungen, d. h. das Polyeder ist leer (z. B. max⁡{x  ∣  x≤1,  x≥2 }\max\{ x \;|\; x \leq 1, \; x \geq 2 \ \}).
  2. das LP ist unbeschränkt, d. h. es gibt Lösungen mit beliebig hohem Zielfunktionswert (z. B. max⁡{x  ∣  x≥0}\max\{ x \;|\; x \geq 0 \}).
  3. es gibt genau eine oder unendliche viele Optimallösungen, die dann alle auf einer gemeinsamen Seitenfläche (Ecke, Kante,...) des Polyeders PP liegen.
Man kann zeigen, dass es immer eine optimale Ecke gibt, falls das Optimierungsproblem überhaupt zulässige Lösungen besitzt und beschränkt ist. Man kann sich also bei der Suche nach Optimallösungen auf die Ecken des Polyeders beschränken, von denen es allerdings sehr viele geben kann.
Die anschauliche Grundidee des Simplex-Verfahrens besteht nun darin, sich schrittweise von einer Ecke des Polyeders zur einer benachbarten Ecke mit besserem Zielfunktionswert zu hangeln, bis es keinen besseren Nachbarn mehr gibt. Da es sich bei der linearen Optimierung um ein konvexes Optimierungsproblem handelt, ist die so gefundene lokal optimale Ecke dann auch global optimal, d. h. es gibt in ganz PP keine andere Ecke mit besserem Zielfunktionswert mehr.

Mathematische Beschreibung des Verfahrens

Das Simplex-Verfahren setzt sich aus zwei Phasen zusammen:
  • Phase I bestimmt eine zulässige Startlösung oder stellt fest, dass das Problem keine Lösung besitzt,
  • Phase II verbessert eine bestehende Lösung immer weiter, bis keine Verbesserung der Zielfunktion mehr möglich ist oder die Unbeschränktheit des Problems festgestellt wird.

Bestimmung einer Startlösung (Phase I)

Zunächst muss eine zulässige Startlösung berechnet werden, bevor man die Phase II starten kann. Eine Möglichkeit dafür ist, für jede Zeile ii eine künstliche Variable ziz_i einzuführen und dann folgendes lineare Programm zu betrachten:
(LP1) min⁡{∑i=1mzi  ∣  Ax+z=b,  x,z≥0}\min \left\{\sum\limits_{i=1}^{m} z_i \;|\; Ax + z = b, \; x,z \geq 0 \right\}.
In einer Optimallösung dieses Hilfsproblems sind die künstlichen Variablen so klein wie möglich, wobei sie immer nichtnegativ bleiben müssen. Das ursprüngliche Problem (LP) besitzt genau dann eine zulässige Lösung, wenn es eine Lösung des Hilfsproblems mit z=0z = 0 gibt, bei der also keine künstlichen Variablen verwendet werden.
Das Hilfsproblem (LP1) besitzt für b≥0b \geq 0 eine einfache zulässige Startlösung, nämlich (x,z)=(0,b)(x,z) = (0,b). Darüber hinaus gilt für jede zulässige Lösung des Hilfsproblems z≤bz \leq b, so dass die Zielfunktion nach oben durch ∑i=1mbi\sum\limits_{i=1}^{m} b_i beschränkt ist. Dieses lineare Programm besitzt also eine Optimallösung, die ausgehend von der Startlösung (0,b)(0,b) mit Phase II des Hilfsproblems bestimmt werden kann. Findet man dabei eine Optimallösung (x∗,z∗)(x^*,z^*) mit z∗=0z^* = 0, ist x∗x^* offensichtlich eine zulässige Startlösung für das Ausgangsproblem (LP), mit der dessen Phase II gestartet werden kann. Gelingt dies nicht, so ist das Ausgangsproblem nicht lösbar, und man kann aufhören.

Bestimmung einer Optimallösung (Phase II)

Phase II ist ein iteratives Verfahren, das in jedem Schritt versucht, aus einer zulässigen Lösung eine neue Lösung mit besserem Zielfunktionswert zu konstruieren, bis dies nicht mehr möglich ist. Dies entspricht im wesentlichen der wiederholten Lösung eines linearen Gleichungssystems mit Hilfe des Gaußschen Eliminationsverfahrens. Dabei kann auch evtl. Unbeschränktheit des Optimierungsproblems festgestellt werden. Zur Erklärung dieser Phase ist die Definition einiger Begriffe notwendig.

Basen, Basislösungen und Ecken

In der Phase II des Simplex-Verfahrens spielt der Begriff der Basis eine wesentliche Rolle. Eine Basis BB von AA ist eine Teilmenge der Spalten von AA, die eine reguläre, also invertierbare Untermatrix ABA_B bilden. Die Variablen, die zu den Basisspalten gehören, heißen Basisvariablen, die anderen Nichtbasisvariablen. Die Basislösung zu einer gegebenen Basis BB ist der eindeutige Vektor xx, dessen Basisvariablen sich als AB−1bA_{B}^{-1} b ergeben und dessen Nichtbasisvariablen alle den Wert 0 haben. Solch eine Basislösung ist also eine zulässige Lösung des Gleichungssystems Ax=bAx = b mit höchstens mm Nicht-Null-Einträgen. In dem Fall, dass alle Komponenten von xx nichtnegativ sind, ist xx auch eine zulässige Lösung von (LP), also ein Punkt des Polyeders PP.
Man kann zeigen, dass jede zulässige Basislösung einer Ecke des Polyeders entspricht und umgekehrt. Eine Basislösung heißt nicht degeneriert, wenn sie genau mm Nicht-Null-Einträge besitzt. In diesem Fall gibt es eine eindeutige zugehörige Basis. Sind alle Basislösungen nicht degeneriert, gibt es also eine bijektive Abbildung zwischen Basen der Matrix AA und Ecken des Polyeders PP.
Ist eine Basislösung dagegen degeneriert, so hat sie weniger als mm Nicht-Null-Einträge und kann zu mehreren Basen gehören. In diesem Fall definiert also jede Basis der Matrix AA genau eine Ecke des Polyeders PP, aber nicht umgekehrt. Dieser Fall tritt auf, wenn eine Ecke von mehr als nn Ungleichungen definiert wird, was bei praktischen Planungsproblemen so gut wie immer der Fall ist.

Iterative Simplexschritte

Die Phase II versucht iterativ in jedem Austauschschritt, aus einer bestehenden Basislösung, wie sie z. B. in Phase I bestimmt wurde, eine neue Basislösung mit mindestens genauso gutem Zielfunktionswert zu konstruieren, indem sie eine Basisvariable aus der Basis entfernt und dafür eine bisherige Nichtbasisvariable in die Basis aufnimmt. Dies wird so lange wiederholt, bis kein verbessernder Austausch mehr möglich ist. In dieser Phase gibt es zu Beginn jeder Iteration ein sogenanntes Simplextableau zur aktuellen Basis BB, in dem die Berechnungen durchgeführt werden. Es entspricht im wesentlichen dem linearen Gleichungsystem Ax=b,  cTx=GAx = b, \; c^T x = G, nach einer Basistransformation in die aktuelle Basis.

Simplextableau

Für die Formulierung des Simplextableaus gibt es unterschiedliche Möglichkeiten. Jeder Simplexschritt geht von einer zulässigen Basis BB aus. Zu Beginn des Schrittes hat das zugehörige Simplextableau die folgende Form:
[cˉ 0∣GAˉ I∣bˉ] \left[ \begin{matrix} \bar{c}\, & 0 &| G\\ \bar{A}\, & I&|\bar{b} \end{matrix} \right] .
Hierbei sind zur Vereinfachung der Darstellung die Spalten so umsortiert worden, dass alle Nichtbasisspalten links stehen und alle Basisspalten rechts. Der (n−m)(n-m)-dimensionale Vektor cˉ\bar{c} und die mm x (n−m)(n-m)-dimensionale Matrix Aˉ\bar{A} sind definiert durch
cˉ=cNT−cBTAB−1AN\bar{c} = c_{N}^{T} - c_{B}^{T} A_{B}^{-1} A_{N},
Aˉ=AB−1AN\bar{A} = A_{B}^{-1} A_{N} und
bˉ=AB−1b\bar{b} = A_{B}^{-1} b.
Dabei ist
  • ABA_{B} die reguläre Untermatrix von AA, die aus den Spalten der aktuellen Basis BB besteht,
  • ANA_{N} die (meistens nicht quadratische) Untermatrix von AA, die aus den Nichtbasisspalten besteht,
  • cBc_{B} bzw. cNc_{N} die Teile des Zielfunktionsvektors cc, die aus den Basis- bzw. Nichtbasisspalten bestehen,
  • II die m-dimensionale Einheitsmatrix,
  • GG der Zielfunktionswert der aktuellen Basislösung.
Die rechte Seite bˉ\bar{b} ist die aktuelle Basislösung, die zur Basis BB gehört. Zu Beginn der Phase I bilden die Variablen ziz_i eine zulässige Basis mit der Einheitsmatrix als Basismatrix und der zugehörigen Basislösung (x,z)=(0,b)(x,z) = (0,b). Daher steht am Anfang auf der rechten Seite einfach der Vektor bb.
Die Einträge des Vektors cˉ\bar{c} heißen reduzierte Kosten der Nichtbasisvariablen. Der Wert cˉj\bar{c}_j gibt die Verbesserung der Zielfunktion an, wenn Variable xjx_j um eine Einheit erhöht wird. Sind zu Beginn eines Simplexschrittes alle reduzierten Kostenkoeffizienten negativ oder 0, sind daher die aktuelle Basis und die zugehörige Basislösung optimal, da die Aufnahme einer bisherigen Nichtbasisvariable in die Basis den Zielfunktionswert verschlechtern würde. Gibt es dagegen Nichtbasisvariablen mit positiven reduzierten Kosten, wird im nächsten Simplexschritt eine von ihnen in die Basis aufgenommen und dafür eine andere Variable aus der Basis entfernt. Wenn die neue Variable innerhalb der Nebenbedingungen Ax=bAx = b erhöht werden kann, verbessert sich der Zielfunktionswert.

Ein einzelner Simplexschritt

Für den eigentlichen Simplexschritt wählt man nun eine Spalte ss der einzufügenden Nichtbasisvariable und eine Zeile rr der aus der Basis zu entfernenden Basisvariablen. Seien aˉij\bar{a}_{ij} die (Matrix-) Elemente des aktuellen Simplextableaus. Dann heißt aˉrs\bar{a}_{rs} das Pivotelement des Simplextableaus. Die Spalte ss heißt Pivotspalte, die Zeile rr heißt Pivotzeile. Ein Austauschschritt entspricht exakt einem Schritt beim Lösen eines linearen Gleichungssystems, bei dem man die Pivotzeile rr nach der Variablen xsx_{s} auflöst und dann xsx_{s} in die restlichen Gleichungen einsetzt. Bei einem Austauschschritt berechnet sich das neue Simplextableau folgendermaßen:
Pivotelement:
aˉrs:=1aˉrs\bar{a}_{rs} := \dfrac{1}{\bar{a}_{rs}} (Formel 1)
Pivotzeile für j ungleich s:
aˉrj:=aˉrjaˉrs\bar{a}_{rj} := \dfrac{\bar{a}_{rj}}{\bar{a}_{rs}} (2)
bˉr:=bˉraˉrs\bar{b}_{r} := \dfrac{\bar{b}_{r}}{\bar{a}_{rs}} (3)
Pivotspalte für i ungleich r:
aˉis:=−aˉisaˉrs\bar{a}_{is} := - \dfrac{\bar{a}_{is}}{\bar{a}_{rs}} (4)
Restliche Elemente der Matrix und reduzierte Kosten:
aˉij:=aˉij−aˉisaˉrjaˉrs\bar{a}_{ij} := \bar{a}_{ij} - \dfrac{\bar{a}_{is} \bar{a}_{rj}}{\bar{a}_{rs}} (5a)
cˉj:=cˉj−cˉscˉjaˉrs\bar{c}_{j} := \bar{c}_{j} - \dfrac{\bar{c}_{s} \bar{c}_{j}}{\bar{a}_{rs}} (5b)
Rechte Seite:
bˉj:=bˉj−bˉraˉjsaˉrs\bar{b}_{j} := \bar{b}_{j} - \dfrac{\bar{b}_{r} \bar{a}_{js}}{\bar{a}_{rs}} (6)
Diese Rechenschritte entsprechen der Anwendung des Gaußschen Eliminationsverfahrens, um die Pivotspalte s im Tableau in einen Einheitsvektor zu transformieren. Dadurch wird die inverse Matrix AB′−1A_{B'}^{-1} zur neuen Basis B′B' nicht komplett neu berechnet, sondern durch Modifikation der alten Basisinversen AB−1A_{B}^{-1} konstruiert.
Ein Simplexschritt, der von einer nicht degenerierten Basislösung ausgeht, führt auf jeden Fall zu einer neuen Basislösung und damit auch zu einer neuen Ecke des Polyeders mit besserem Zielfunktionswert. Ist dagegen die Basislösung degeneriert, kann es passieren, dass die neue Basis nach dem Simplexschritt zur selben Basislösung und damit auch zur selben Ecke gehört, so dass der Zielfunktionswert sich nicht ändert. Bei unvorsichtiger Wahl der Pivotelemente kann es zu sogenannten Zyklen kommen, bei der reihum immer wieder dieselben Basen besucht werden, so dass der Algorithmus in eine Endlosschleife läuft. Dies lässt sich aber beispielsweise durch eine geeignete Auswahl der Pivotzeile verhindern. In der Praxis ist eine weitere Methode, mit Zykeln umzugehen, eine absichtliche Perturbation (numerische Störung) der Daten, die nach einigen Iterationen wieder rausgerechnet wird, wenn der Algorithmus die betreffende Ecke verlassen hat.
Für die Wahl des Pivotelements gibt es meist mehrere Möglichkeiten. Die ursprünglich von Dantzig vorgeschlagene Methode wählt eine der Spalten mit dem größten reduzierten Kostenwert und eine beliebige Zeile, bei der nach dem Simplexschritt wieder eine zulässige (insbesondere nichtnegative) Basislösung entsteht. Dazu muss bei gegebener Pivotspalte ss eine Pivotzeile gewählt werden, bei der das Minimum
λ:=min⁡{bˉiaˉis∣  i=1,…,m, aˉis>0}\lambda := \min \left\{ \dfrac{\bar{b}_{i}}{\bar{a}_{is}} \vert \; i=1,\ldots,m, \, \bar{a}_{is} > 0 \right\}
angenommen wird. Sind alle Einträge in Spalte ss negativ, ist das Optimierungsproblem unbeschränkt, da man Lösungen mit beliebig gutem Zielfunktionswert konstruieren könnte. In diesem Fall kann man aufhören.
Im Normalfall gibt es sowohl mehrere Spalten mit positiven reduzierten Kosten als auch mehrere Zeilen, bei denen das Minimum λ\lambda angenommen wird, so dass eine Wahlmöglichkeit besteht. Da die Wahl des Pivotelements einen großen Einfluss auf die Rechenzeit haben kann, sind innerhalb der letzten 60 Jahre zahlreiche verbesserte Pivotstrategien gegenüber der Lehrbuchvariante entwickelt worden (siehe unten).

Duale Information im Tableau

Aus dem Simplextableau lässt sich auch die Information zur Lösung des zu dem linearen Programm (LP) gehörigen dualen linearen Programms entnehmen. Zu einer gegebenen Basis BB kann man neben der zugehörigen Primallösung x=bˉ=AB−1bx = \bar{b} = A_{B}^{-1} b, die in der rechten Spalte des Tableaus steht, auch eine Duallösung π=cBTAB−1\pi = c_{B}^{T} A_{B}^{-1} berechnen. Diese beiden Vektoren xx und π\pi erfüllen immer die Bedingung
πTb=cTx\pi^{T} b = c^{T} x,
die für Optimallösungen notwendig ist. Der Vektor xx bleibt nach Konstruktion der einzelnen Simplexiterationen immer zulässig für das primale LP, während der Vektor π\pi Bedingungen des dualen LPs verletzen kann. Sind zu einer Basis sowohl die zugehörige Primallösung xx als auch die entsprechende Duallösung π\pi zulässig (man spricht dann von einer primal und dual zulässigen Basis), dann sind beide optimal für das primale bzw. duale lineare Programm. Man kann zeigen, dass dies genau dann der Fall ist, wenn der reduzierte Kostenvektor cˉ\bar{c} nichtpositiv ist. Obwohl das Ziel des Simplex-Verfahrens eigentlich nur die Berechnung einer optimalen Primallösung ist, fällt also am Ende auch eine optimale Duallösung nebenbei mit ab.

Literatur

  • George B. Dantzig: Lineare Programmierung und Erweiterungen. Springer-Verlag 1966 (Originalausgabe: Linear Programming and Extensions, Princeton University Press, ISBN 0-691-05913-6.)
  • V. Klee und G.J. Minty: How Good is the Simplex Algorithm? In: O. Shisha, editor, Inequalities III, Seiten 159-175. Academic Press, New York, 1972
  • Vašek Chvátal: Linear Programming. W. H. Freeman and Company, New York, 1983, ISBN 0-716-71587-2.
  • Alexander Schrijver: Theory of Linear and Integer Programming. John Wiley and Sons. 1998, ISBN 0-471-98232-6.
  • Wolfgang Domschke, Andreas Drexl: Einführung in Operations Research. 6. Auflage. Springer, Berlin 2005, ISBN 3-540-23431-4
 
 

Manche Menschen haben einen Gesichtskreis vom Radius Null und nennen ihn ihren Standpunkt.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Simplex-Verfahren aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Optimierung