Konvexe Optimierung

Die Konvexe Optimierung ist ein Teilgebiet der mathematischen Optimierung. Es ist eine bestimmte Größe zu minimieren, die sogenannte Zielfunktion, welche von einem Parameter, welcher mit xx bezeichnet wird, abhängt. Außerdem sind bestimmte Nebenbedingungen einzuhalten, d.h. die Werte xx, die man wählen darf, sind gewissen Einschränkungen unterworfen. Diese sind meist in Form von Gleichungen und Ungleichungen gegeben. Sind für einen Wert xx alle Nebenbedingungen eingehalten, so sagt man, dass xx zulässig ist. Man spricht von einem konvexen Optimierungsproblem oder einem konvexen Programm, falls sowohl die Zielfunktion als auch die Menge der zulässigen Punkte konvex ist. Viele Probleme der Praxis sind konvexer Natur. Oft wird zum Beispiel auf Quadern optimiert, welche stets konvex sind, und als Zielfunktion finden oft quadratische Formen Verwendung, die unter bestimmten Voraussetzungen ebenfalls konvex sind. Ein anderer wichtiger Spezialfall ist die Lineare Optimierung, bei der eine lineare Zielfunktion über einem konvexen Polyeder optimiert wird.
Eine wichtige Eigenschaft der konvexen Optimierung im Unterschied zur nicht-konvexen Optimierung ist, dass jedes lokale Optimum auch ein globales Optimum ist. Anschaulich bedeutet dies, dass eine Lösung, die mindestens so gut ist wie alle anderen Lösungen in einer Umgebung, auch mindestens so gut ist wie alle zulässigen Lösungen. Dies erlaubt es, einfach nach lokalen Optima zu suchen.

Einleitung

Es gibt viele mögliche Formulierungen eines konvexen Programms. An dieser Stelle soll eine möglichst allgemeine Form gewählt werden. Der Eingabeparameter xx sei aus dem Rn\R^n, d.h. das Problem hängt von nn Einflussparametern ab. Die Zielfunktion f:K→Rf:K\rightarrow\R sei konvex. Weiterhin seien die konvexen Funktionen gi:K→Rg_i :K\rightarrow\R mit 1≤i≤m1 \leq i \leq m und die affinen Funktionen hj:K→Rh_j :K\rightarrow\R mit 1≤j≤l1 \leq j \leq l gegeben. Hierbei ist KK eine konvexe Teilmenge des Rn\R^n.
Konvexes Programm:
Minimiere f(x)f(x) mit x∈Kx\in K unter den Nebenbedingungen
gi(x)≤0 ,1≤i≤mg_i (x)\leq 0 ~ ,1 \leq i \leq m
hj(x)=0 ,1≤j≤lh_j (x) = 0 ~, 1 \leq j \leq l
Eine Restriktion mit gi(x)=0g_i (x)= 0 bezeichnet man als aktiv. Die Funktionen gig_i stellen die sogenannten Ungleichungsnebenbedingungen und die Funktionen hjh_j stellen die sogenannten Gleichungsnebenbedingungen dar.

Beispiel

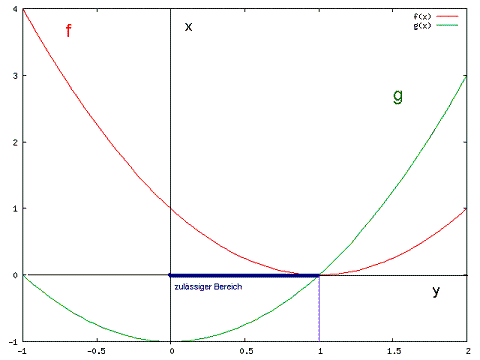
KonvexeOptimierung_beispiel.png
Konvexes Optimierungsproblem
Als Beispiel wird ein eindimensionales Problem ohne Gleichungsnebenbedingungen und mit nur einer Ungleichungsnebenbedingung betrachtet:
Minimiere f(x)=(x−1)2f(x)=(x-1)^2 mit x∈K=[0,∞)x\in K=[0,\infty) unter der Nebenbedingung:
g(x)=x2−1≤0g(x)= x^2 - 1 \leq 0
Der zulässige Bereich ist gegeben durch die konvexe Menge
{x∈K:g(x)≤0}=[0,1]\{x\in K:g(x)\leq 0\}=[0,1].
Der Zeichnung entnimmt man, dass für x=1x = 1 der Optimalwert 00 angenommen wird.

Optimalitätsbedingungen

Zunächst werden notwendige Optimalitätsbedingungen vorgestellt. Dies sind Kriterien, die auf jeden Fall im Optimum x^\hat{x} erfüllt sein müssen. Danach werden hinreichende Optimalitätsbedingungen formuliert. Diese zeigen, dass eine Lösung x^\hat{x} wirklich optimal ist.

Fritz-John-Bedingungen

Sei x^\hat{x} optimal für das obige konvexe Programm. Dann gibt es Multiplikatoren λ, μ1,…,μm, ν1,…,νl\lambda,~\mu_1,\ldots,\mu_m,~\nu_1,\ldots,\nu_l, die nicht sämtlich den Wert 00 haben, mit den folgenden Eigenschaften:
  • λ, μ1,…,μm≥0\lambda,~\mu_1,\ldots,\mu_m\geq 0
  • gi(x^)<0⇒μi=0 ,1≤i≤mg_i (\hat{x}) <0 \Rightarrow \mu_i=0~ , 1 \leq i \leq m (Complementary slackness condition)
  • λf(x^)+∑i=1mμigi(x^)+∑j=1lνjhj(x^)≤λf(x)+∑i=1mμigi(x)+∑j=1lνjhj(x)\lambda f(\hat{x})+\sum\limits_{i=1}^m \mu_i g_i(\hat{x})+\sum\limits_{j=1}^l \nu_j h_j(\hat{x}) \leq \lambda f(x)+\sum\limits_{i=1}^m \mu_i g_i(x)+\sum\limits_{j=1}^l \nu_j h_j(x) für alle x∈Kx\in K
Die Fritz-John-Bedingungen sind ein notwendiges Optimalitätskriterium. Für λ>0\lambda>0 sind sie hinreichend. In diesem Fall darf man sogar λ=1\lambda=1 setzen. Die complementary slackness condition wird im Deutschen auch Bedingung vom komplementären Schlupf genannt. Hierbei kann man beweisen, dass falls gi(x^)<0g_i (\hat{x}) <0 für alle 1≤i≤m1 \leq i \leq m gilt, dass dann alle Multiplikatoren μi=0\mu_i=0 für alle 1≤i≤m1 \leq i \leq m sein müssen. Diese Bedingung ist somit für den Aufbau und den Entwurf von Algorithmen von hoher Bedeutung.

Karush-Kuhn-Tucker-Bedingungen

Die Karush-Kuhn-Tucker-Bedingungen (auch bekannt als die KKT-Bedingungen) sind notwendig für die Optimalität einer Lösung in der nichtlinearen Optimierung. Sie stellen eine Verallgemeinerung der Lagrangen Multiplikatoren dar.

Notwendige Bedingungen

Sei f:K→Rf:K\rightarrow\R die Zielfunktion und die konvexen Funktionen gi:K→Rg_i :K\rightarrow\R mit 1≤i≤m1 \leq i \leq m und die affinen Funktionen hj:K→Rh_j :K\rightarrow\R mit 1≤j≤l1 \leq j \leq l sind Nebenbedingungs-Funktionen. Es sei x^\hat{x} ein zulässiger Punkt, d.h. es gilt x^∈K\hat{x} \in K. Des Weiteren nimmt man an, dass die aktiven Funktionen gig_i differenzierbar im Punkt x^\hat{x} sind, die Funktionen hjh_j sind stetig differenzierbar im Punkt x^∈K\hat{x} \in K. Falls x^\hat{x} ein lokales Minimum ist, dann existieren Konstanten λ≥0, μi≥0\lambda \ge 0,\, \mu_i \ge 0 mit 1≤i≤m1 \leq i \leq m und νj\nu_j mit 1≤j≤l,1 \leq j \leq l, so dass
λ+∑i=1mμi+∑j=1l∣νj∣>0,\lambda + \sum\limits_{i=1}^m \mu_i + \sum\limits_{j=1}^l |\nu_j| > 0,
λ∇f(x^)+∑i=1mμi∇gi(x^)+∑j=1lνj∇hj(x^)=0,\lambda\nabla f(\hat{x}) + \sum\limits_{i=1}^m \mu_i \nabla g_i(\hat{x}) + \sum\limits_{j=1}^l \nu_j \nabla h_j(\hat{x}) = 0,
μigi(x^)=0\mu_i g_i (\hat{x}) = 0 für alle 1≤i≤m 1 \leq i \leq m\,
Außerdem gilt
f(x^)+∑i=1mμigi(x^)≤f(x)+∑i=1mμigi(x)f(\hat{x})+\sum\limits_{i=1}^m \mu_i g_i(\hat{x}) \leq f(x)+\sum\limits_{i=1}^m \mu_i g_i(x) für alle x∈K x\in K
und die Komplementaritätsbedingung ist erfüllt:
gi(x^)<0⇒μi=0 ,1≤i≤mg_i (\hat{x}) <0 \Rightarrow \mu_i=0~ , 1 \leq i \leq m

Regularitäts-Bedingungen

Für die obige notwendige Bedingung darf das duale Skalar λ\lambda gleich Null sein. In solchen Fällen spricht man von degeneriert oder abnormal. Dann spielt die notwendige Bedingung keine Rolle für die Eigenschaften der Funktion, nur die Geometrie der Nebenbedingungen ist relevant.
Es existieren mehrere Bedingungen, welche sicherstellen, dass die Lösung nicht-degeneriert ist, d.h. λ≠0\lambda \ne 0. Diese werden Constraint Qualifications genannt.

Hinreichende Bedingungen

Sei f:K→Rf:K\rightarrow\R die Zielfunktion und die konvexen Funktionen gi:K→Rg_i :K\rightarrow\R mit 1≤i≤m1 \leq i \leq m und die affinen Funktionen hj:K→Rh_j :K\rightarrow\R mit 1≤j≤l1 \leq j \leq l sind Nebenbedingungs-Funktionen. Es sei x^\hat{x} ein zulässiger Punkt, d.h. es gilt x^∈K\hat{x} \in K. Des Weiteren nimmt man an, dass die aktiven Gradienten ∇gi(x^)\nabla g_i(\hat{x}) und die Gradienten ∇hj(x^)\nabla h_j(\hat{x}) linear unabhängig sind. Falls x^\hat{x} ein lokales Minimum ist, dann existieren Konstanten λ≥0, μi≥0\lambda \ge 0,\, \mu_i \ge 0 mit 1≤i≤m1 \leq i \leq m und νj\nu_j mit 1≤j≤l,1 \leq j \leq l, so dass
∇f(x^)+∑i=1mμi∇gi(x^)+∑j=1lνj∇hj(x^)=0\nabla f(\hat{x}) + \sum\limits_{i=1}^m \mu_i \nabla g_i(\hat{x}) + \sum\limits_{j=1}^l \nu_j \nabla h_j(\hat{x}) = 0
μigi(x^)=0\mu_i g_i (\hat{x}) = 0 für alle 1≤i≤m1 \leq i \leq m
dann ist der Punkt x^\hat{x} ein globales Minimum.

Constraint Qualifications

Ein Kriterium, welches sicherstellt, dass λ>0\lambda>0 gilt, nennt man Constraint Qualification. Mit anderen Worten, eine Bedingung, die sicherstellt, dass die Fritz-John-Bedingungen auch die Karush-Kuhn-Tucker-Bedingungen erfüllen, nennt man Constraint Qualification.
Beispiele für Constraint Qualifications sind:
  • Slater: Es treten keine Gleichungsnebenbedingungen auf. Des weiteren gibt es einen Punkt x~∈K\tilde{x}\in K, so dass gi(x~)<0g_i (\tilde{x})<0 für alle 1≤i≤m1 \leq i \leq m. An dieser Stelle sei erwähnt, dass die Constraint Qualification von Slater im Allgemeinen als die wichtigste angesehen wird.
  • Lineare Unabhängigkeit - Linear independence constraint qualification (LICQ): Die Gradienten der aktiven Ungleichungsbedingungen und die Gradienten der Gleichungsbedingungen sind linear unabhängig im Punkt x^\hat{x}.
  • Mangasarian-Fromowitz - Mangasarian-Fromowitz constraint qualification (MFCQ): Die Gradienten der aktiven Ungleichungsbedingungen und die Gradienten der Gleichungsbedingungen sind positiv-linear unabhängig im Punkt x^\hat{x}.
  • Konstanter Rang - Constant rank constraint qualification (CRCQ): Für jede Untermenge der Gradienten, der Ungleichungsbedingungen, welche aktiv sind, und der Gradienten der Gleichungsbedingungen ist der Rang in der Nähe von x^\hat{x} konstant.
  • Konstante positive-lineare Abhängigkeit - Constant positive-linear dependence constraint qualification (CPLD): Für jede Untermenge der Gradienten, der Ungleichungsbedingungen, welche aktiv sind, und der Gradienten der Gleichungsbedingungen, und falls eine positive-lineare Abhängigkeit im Punkt x^\hat{x} vorliegt, dann gibt es eine positiv-lineare Abhängigkeit in der Nähe von x^\hat{x}.
Man kann zeigen, dass die Folgerungen gelten
LICQ⇒MFCQ⇒CPLD\text{LICQ} \Rightarrow \text{MFCQ} \Rightarrow \text{CPLD} und LICQ⇒CRCQ⇒CPLD\text{LICQ} \Rightarrow \text{CRCQ} \Rightarrow \text{CPLD},
obwohl MFCQ nicht äquivalent zu CRCQ ist. In der Praxis werden schwächere Constraint Qualifications bevorzugt, da diese stärkere Optimalitäts-Bedingungen liefern.

Konkretes Vorgehen

Lagrange-Funktion

Zunächst wird die folgende abkürzende Schreibweise eingeführt:
L(x,λ)=f(x)+∑i=1mμigi(x)+∑j=1lνjhj(x)L(x,\lambda)=f(x)+\sum\limits_{i=1}^m \mu_i g_i(x)+\sum\limits_{j=1}^l \nu_j h_j(x),
wobei λ\lambda der Vektor aus allen Multiplikatoren ist.

Lagrangesche Multiplikatorenregel für das konvexe Problem

Vergleiche hierzu auch mit Lagrangesche Multiplikatorenregel. Konkretes Vorgehen:
  • Überprüfe, ob alle auftretenden Funktionen stetig partiell differenzierbar sind. Falls nein, ist diese Regel nicht anwendbar.
  • Gibt es einen zulässigen Punkt x^\hat{x}, für den gilt: ∇f(x^)=0\nabla f(\hat{x})=0? Falls ja, dann ist x^\hat{x} optimal. Sonst fahre mit dem nächsten Schritt fort.
  • Bestimme den Gradienten ∇xL(x,λ)\nabla_x L(x,\lambda) der Lagrange-Funktion.
  • Löse das System ∇xL(x,λ)(x−x^)≥0 (x∈K)\nabla_x L(x,\lambda)(x-\hat{x})\geq 0~(x\in K), wobei kein Multiplikator negativ sein darf. Falls eine Restriktion aktiv ist, muss der zugehörige Multiplikator sogar gleich 00 sein. Findet man eine Lösung x^\hat{x}, so ist diese optimal.

Literatur

  • Avriel, Mordecai: Nonlinear Programming: Analysis and Methods. Dover Publishing, 2003, ISBN 0-486-43227-0.
  • R. Andreani, J. M. Martínez, M. L. Schuverdt: On the relation between constant positive linear dependence condition and quasinormality constraint qualification. Journal of optimization theory and applications, vol. 125, no2, 2005, pp. 473-485.
  • F. Jarre, J. Stoer: Optimierung. Springer, Berlin 2003, ISBN 3-540-43575-1.
 
 

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Konvexe Optimierung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerik