Eulerkreisproblem
Ein Eulerkreis oder (geschlossener) Eulerzug (auch Eulertour oder Eulersche Linie) ist in der Graphentheorie ein Zyklus, der alle Kanten eines Graphen genau einmal enthält. Ein offener Eulerzug oder Eulerweg ist dann gegeben, wenn die Identität von Start- und Endknoten nicht verlangt wird, d.h. statt eines Zyklus wird lediglich ein Weg verlangt, der jede Kante des Graphen genau einmal enthält. Einen zusammenhängenden Graph, der einen Eulerkreis besitzt, bezeichnet man auch als eulersch.
Die Aufgabe, zu einem gegebenen Graph zu bestimmen, ob dieser eulersch ist oder nicht, bezeichnet man als Eulerkreis-Problem. Es geht auf das 1736 von Leonhard Euler gelöste Königsberger Brückenproblem zurück. Das Problem existiert auch für gerichtete Graphen und Graphen mit Mehrfachkanten.
Eigenschaften
Für ungerichtete Graphen sind folgende Aussagen äquivalent:
- ist eulersch,
- ist zusammenhängend und jeder Knoten hat geraden Grad.
- ist zusammenhängend und die Kantenmenge von ist die Vereinigung aller Kanten von paarweise disjunkten Kreisen.
Analog sind für gerichtete Graphen folgende Aussagen äquivalent:
- ist eulersch,
- ist stark zusammenhängend und für jeden Knoten sind Eingangsgrad und Ausgangsgrad äquivalent.
- ist stark zusammenhängend und die Kantenmenge von ist die Vereinigung aller Kanten von paarweise disjunkten gerichteten Kreisen.
Verallgemeinerung: Eulerweg
Ein (ungerichteter zusammenhängender) Graph enthält genau dann einen Eulerweg, wenn zwei oder keiner seiner Knoten von ungeradem Grad ist; hat kein Knoten ungeraden Grad, handelt es sich bei dem Eulerweg um einen Eulerkreis.
Lösung
Das Problem lässt sich relativ leicht algorithmisch lösen, da ein Graph genau dann eulersch ist, wenn er zusammenhängend ist und jeder Knoten geraden Grad besitzt. Mittels Tiefensuche lässt sich dies leicht in linearer Zeit feststellen. Zu einem Eulerschen Graphen einen Eulerkreis zu finden erfordert dagegen einen etwas komplizierteren Algorithmus, der auch auf Tiefensuche basiert und dieses Problem ebenfalls in Linearzeit lösen kann. Den ersten Linearzeit-Algorithmus dafür konnte Hierholzer angeben, der ausnutzte, dass Eulersche Graphen auch dadurch charakterisiert werden können, dass sie aus kantendisjunkten Kreisen zusammengesetzt werden können.
Anwendungsbeispiele
Das Königsberger Brückenproblem
Das Königsberger Brückenproblem lässt sich in folgendem Graphen ausdrücken:
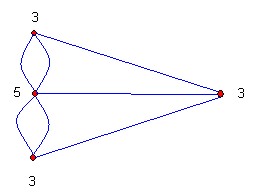
Graph für das Königsberger Brückenproblem
Die roten Punkte (Knoten) sind die jeweiligen Stadtteile bzw. Standpunkte. Die blauen Linien (Kanten) sind die Brücken. Durch Probieren wird man herausfinden, dass es nicht möglich ist, alle Stadtteile hintereinander zu besuchen und jede Brücke nur ein einziges Mal zu benutzen. Es gibt also keinen Eulerweg und demzufolge auch keinen Eulerkreis. Warum ist das so?
Euler hat die folgende Gesetzmäßigkeit entdeckt: Wenn in einem Graphen ein Eulerweg existiert, dann haben maximal 2 Knoten ungeraden Grad (also haben nicht mehr als zwei Knoten eine ungerade Anzahl angeschlossener Kanten). Beim Königsberger Brückengraphen gibt es vier Knoten mit ungeradem Grad (die Zahlen neben den Knoten geben hier deren Grad an). Deshalb ist der Stadtrundgang mit dem nur einmaligen Benutzen jeder Brücke unmöglich.
"Das-ist-das-Haus-vom-Nikolaus"
Das beliebte Kinderrätsel "Das ist das Haus vom Nikolaus" hingegen enthält einen Eulerweg, aber keinen Eulerkreis, da sein Graph Knoten vom Grad 3 enthält.
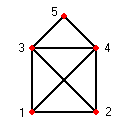
Das ist das Haus vom Nikolaus
Ein Eulerweg ist z.B. 1-2-4-3-1-4-5-3-2.
Ein Quadrat mit Diagonalen enthält keinen Eulerweg, da alle seine Knoten den Grad 3 haben. (Im Bild sind das nur die Punkte 1,2,3,4 mit den verbindenden Kanten.)
Siehe auch
Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis.
Jean-Baptist le Rond d'Alembert
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Eulerkreisproblem
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе