Hamiltonkreisproblem

Das Hamiltonkreisproblem ist eine der fundamentalen Problemstellungen der Graphentheorie. Es fragt, ob in einem gegebenen Graph ein sogenannter Hamiltonkreis existiert. Ein Hamiltonkreis ist dabei ein Kreis, der alle Knoten des Graphen enthält.
Man unterscheidet zwei grundlegende Varianten des Problems. Beim gerichteten Hamiltonkreisproblem fragt man nach der Existenz eines gerichteten Hamiltonkreis in einem gerichteten Graphen. Entsprechend fragt man beim ungerichteten Hamiltonkreisproblem nach der Existenz eines ungerichteten Hamiltonkreis in einem ungerichteten Graphen.
 
 

Geschichte

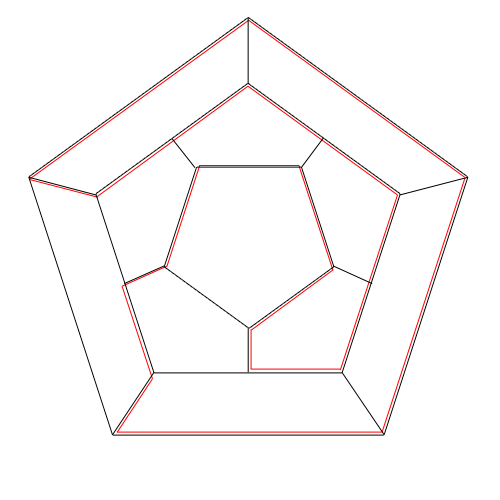
Hamcyc.png
Das Dodekaeder, wie alle platonischen Körper, ist hamiltonisch.
Namensgeber des Problems ist der irische Astronom und Mathematiker Sir William Rowan Hamilton, der 1857 das Spiel "The Icosian Game" erfand (und später verbesserte zum "Traveller's Dodecahedron or A Voyage Round The World").
Der "Traveller's Dodecahedron" besteht aus einem hölzernen, regulären Dodekaeder, wobei die 20 Knoten mit Namen bekannter Städte assoziiert sind. Ziel ist es, eine Reiseroute entlang der Kanten des Dodekaeders zu finden, die jede Stadt genau einmal besucht und dort aufhört, wo sie beginnt.
Zunächst erscheint die Aufgabenstellung ähnlich dem 1736 von L. Euler (verneinend) gelösten Königsberger Brückenproblem, einem Spezialfall des Eulerkreisproblems und Grundsteinlegung der Graphentheorie. Während für das Eulerkreisproblem aber besonders effiziente Lösungs-Algorithmen existieren ist bekannt, dass beide Varianten des Hamiltonkreisproblems besonders schwer algorithmisch lösbare Probleme sind. Sowohl die gerichtete als auch die ungerichtete Variante des Hamiltonkreisproblems gehört zur Liste der 21 klassischen NP-vollständigen Probleme, für die Richard Karp 1972 in seinem berühmten Artikel die Zugehörigkeit zu dieser Klasse von Problemen nachgewiesen hat.

Definitionen

Sei G=(V,E)G=(V,E) ein Graph mit ∣V∣=n|V|=n Knoten (oder Ecken) und ∣E∣=m|E|=m Kanten.
GG ist hamiltonisch, wenn er einen Hamiltonkreis zulässt, d.h., wenn es einen Kreis in GG gibt, der alle Knoten aus VV enthält. Ein Hamiltonpfad ist ein Pfad in GG, der alle Knoten aus VV enthält. Hat GG Hamiltonpfade, jedoch keinen Hamiltonkreis, so ist GG semihamiltonisch.
Zur Potenz eines Graphen: Für einen Graphen GG und d∈Nd \in \mathbb{N} bezeichnet GdG^d den Graphen auf VV, bei dem zwei Knoten genau dann benachbart sind, wenn sie in GG einen Abstand (oder Distanz) ≤d\leq d haben. Offenbar gilt G=G1⊆G2⊆G3⊆…G=G^1\subseteq G^2\subseteq G^3\subseteq\dots .
Ist GG ein Graph mit nn Knoten und Knotengraden d1≤…≤dnd_{1}\leq\dots \leq d_{n}, so nennt man das Tupel (d1,…,dn)(d_{1},\dots ,d_{n}) die Gradsequenz (oder Valenzfolge) von GG, welche eindeutig bestimmt ist. Ein beliebiges Tupel (a1,…,an)(a_{1},\dots ,a_{n}) natürlicher Zahlen heißt hamiltonisch, wenn jeder Graph mit nn Knoten und punktweise größerer Gradsequenz hamiltonisch ist. (Eine Gradsequenz (d1,…,dn)(d_{1},\dots ,d_{n}) ist punktweise größer als (a1,…,an)(a_{1},\dots ,a_{n}), wenn di≥aid_{i}\geq a_{i} gilt für alle ii.)

Wichtige Aussagen und Sätze

Welche Bedingungen an einen Graphen GG mit n≥3n\geq 3 haben die Existenz eines Hamiltonkreises zur Folge? Besonders wichtige Theoreme sind chronologisch aufgelistet:

Sätze

G. A. Dirac (1952), der historische Ausgangspunkt der Entdeckung einer ganzen Reihe von Bedingungen: Jeder Graph GG mit mindestens Minimalgrad n2\dfrac{n}{2} hat einen Hamiltonkreis.
W. T. Tutte (1956):
Jeder 4-zusammenhängende planare (oder plättbare) Graph hat einen Hamiltonkreis.
Ø. Ore (1960):
Ist die Summe des Grades (oder Valenz) zweier nicht-adjazenter Knoten mindestens nn, so ist GG hamiltonisch.
Ø. Ore (1960):
Ist die Summe der Grade zweier nicht-adjazenter Knoten x,yx,y mindestens nn, so gilt: G+{x,y}G+\{x,y\} hamiltonisch ⇒G\Rightarrow G hamiltonisch.
L. Pósa (1962) mit einer Verallgemeinerung früherer Ergebnisse von G. A. Dirac und Ø. Ore:
Wenn für jedes p, 1≤p<n−12p,\, 1\leq p<\dfrac{n-1}{2}, die Anzahl der Knoten von Grad ≤p\leq p kleiner als pp und für ungerade nn, die Anzahl der Knoten von Grad ≤n−12\leq \dfrac{n-1}{2} nicht größer als n−12\dfrac{n-1}{2} gilt, so ist GG hamiltonisch.
V. Chvátal (1972): Ein Tupel (a1,…,an)(a_{1},\dots ,a_{n}) natürlicher Zahlen mit a1≤…≤an<na_{1}\leq\dots \leq a_{n}<n ist genau dann hamiltonisch, wenn für jedes i<n2i<\dfrac{n}{2} gilt: ai≤i⇒an−i≥n−ia_{i}\leq i \Rightarrow a_{n-i}\geq n-i.
V. Chvátal & P. Erdös (1972): Ist GG k-zusammenhängend und die Mächtigkeit jeder Menge unabhängiger Knoten aus GG ≤k\leq k, so ist GG hamiltonisch.
H. Fleischner (1974): Ist GG 2-zusammenhängend, so hat G2G^2 einen Hamiltonkreis.
J. A. Bondy & V. Chvátal (1976):
GG ist genau dann hamiltonisch, wenn sein Hamiltonabschluss hamiltonisch ist.

Weitere hinreichende Eigenschaften

  • Jeder vollständige Graph mit n≥3n\geq 3 ist hamiltonisch.
  • GG ist hamiltonisch, falls GG Kantengraph eines Eulerschen oder hamiltonischen Graphen ist.
  • GG ist genau dann hamiltonisch, wenn GG einen Teilgraphen - bei dem nur Kanten entfernt wurden - besitzt, der Kantengraph eines Eulerschen oder hamiltonischen Graphen ist.
  • Die Knotenzusammenhangszahl von GG ist mindestens so groß wie die Stabilitätszahl (oder Unabhängigkeitszahl) von GG.
  • Jeder panzyklische Graph ist hamiltonisch.

Notwendige Kriterien

Nach der Vorstellung hinreichender Bedingungen nun eine Auswahl notwendiger Kriterien für die Existenz von Hamiltonkreisen. Besitzt GG einen Hamiltonkreis, so gilt:
  • GG besitzt keinen Schnittknoten,
  • GG besitzt keine Brücke,
  • der Blockgraph von GG ist ein isolierter Knoten,
  • GG besitzt einen 2-Faktor,
  • GG ist 2-zusammenhängend,
  • der Minimalgrad ist mindestens 2 und
  • der Durchmesser von GG ist höchstens n2\dfrac{n}{2}.

Vermutungen

In diesem Zusammenhang wurden diese wichtigen - nicht allgemein gelösten - Vermutungen geäußert:
D. W. Barnette (1969):
Jeder 3-zusammenhängende bipartite kubische planare Graph ist hamiltonisch.
P. Seymour (1974):
Ist der Minimalgrad von GG δ(G)≥kk+1n\delta(G)\geq \dfrac{k}{k+1}n, so hat GG einen Hamiltonkreis HH mit Hk⊆GH^k \subseteq G. Für k=1k=1 entspricht dies dem Satz von G. A. Dirac, 1952. Die Aussage für k=2k=2 war bereits 1963 von L. Pósa vermutet worden und wurde 1996 für hinreichend große nn von J. Komlós, G. N. Sárközy & E. Szemerédi bewiesen.

Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Hamiltonkreisproblem aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Graphentheorie