Königsberger Brückenproblem
Das Königsberger Brückenproblem ist ein 1736 von Leonhard Euler gelöstes mathematisches Problem. Am konkreten Beispiel bezieht es sich auf die Stadt Königsberg und die Frage, ob es einen Rundweg gibt, bei dem man alle sieben Brücken der Stadt über den Pregel genau einmal überquert und wieder zum Ausgangspunkt gelangt. Euler bewies, dass es keinen solchen Rundweg geben kann.
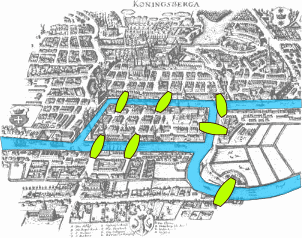
Das Königsberger Brückenproblem
Das Brückenproblem ist kein klassisches geometrisches Problem, da es nicht auf die genaue Lage der Brücken ankommt, sondern nur darauf, welche Brücke welche Inseln miteinander verbindet. Es handelt sich deshalb um ein topologisches Problem, das Euler mit Methoden löste, die wir heute der Graphentheorie zurechnen.
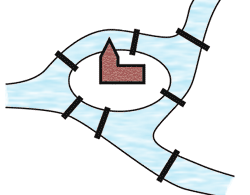
Schematische Darstellung
Euler zeigte, dass ein Rundweg der gesuchten Art genau dann möglich ist, wenn sich an keinem der Ufer (Knoten) eine ungerade Zahl von Brücken (Kanten) befindet. Da aber zu allen vier Gebieten von Königsberg eine ungerade Zahl von Brücken führten, war der gesuchte Rundweg nicht möglich.
Das Problem lässt sich auf beliebige Graphen und die Frage, ob es darin einen Zyklus gibt, der alle Kanten genau einmal benutzt, verallgemeinern. Ein solcher Zyklus wird als Eulerkreis bezeichnet und ein Graph, der einen Eulerkreis besitzt, als eulersch.
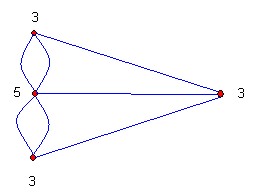
Darstellung als Graph
Die Frage, ob ein Graph eulersch ist, lässt sich relativ einfach beantworten und ist auch in gerichteten Graphen und Graphen mit Mehrfachkanten möglich.
Im heutigen Königsberg/ Kaliningrad ist es aufgrund anderer Brücken möglich einen Eulerweg, aber keinen Eulerkreis über die Brücken zu beschreiben.
Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.
Leonardo da Vinci
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Königsberger Brückenproblem
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе
Graphentheorie
- Typen von Graphen
- Nachbarschaft und Grad
- Wege, Pfade, Zyklen und Kreise
- Isomorphie von Graphen
- Operationen auf Graphen
- Zusammenhang
- Durchlaufbarkeit von Graphen
- Eulerkreisproblem
- Königsberger Brückenproblem
- Briefträgerproblem
- Hamiltonkreisproblem
- Problem des Handlungsreisenden
- Färbung
- Paarungen in Graphen
- Schnitte
- Knotenüberdeckungen, Cliquen und stabile Mengen