Beispiele für Distributionen

Sei Ω⊆R\Omega \subseteq \R und f∈C(Ω) f \in C(\Omega), so ist durch T(φ):=∫−∞∞f(x)φ(x)dxT(\phi):=\int\limits_{-\infty}^\infty f(x) \phi(x) d x für alle φ∈Cc∞(Ω)\phi \in C_c^\infty(\Omega) eine Distribution T∈D′(Ω)T \in \mathcal{D}'(\Omega) definiert.

Delta-Distribution

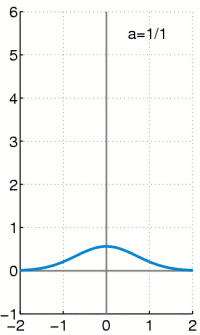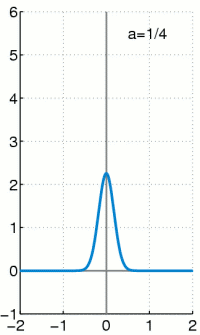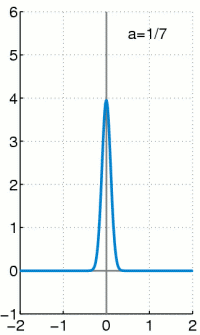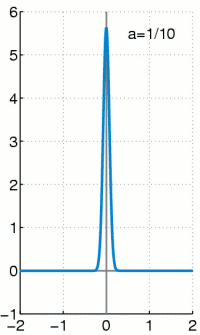
Dirac_function_approximation.gif
Die Delta-Distribution wird durch die Funktionenfolge δa(x)=12πa⋅e−x22a\textstyle \delta_{a}(x)=\dfrac {1}{\sqrt{2\pi a}} \cdot e^{-\dfrac {x^2}{2a}} approximiert. Für alle aa bleibt der Flächeninhalt unter der Funktion gleich Eins.
Die Delta-Distribution δ\delta ist eine singuläre Distribution. Das heißt, sie kann nicht durch eine gewöhnliche Funktion erzeugt werden, obwohl sie oft wie eine solche geschrieben wird. Es gilt:
δ(φ):=φ(0)    \delta (\phi) := \phi (0)\, \;
Das heißt, die Delta-Distribution angewendet auf eine Testfunktion φ\phi ergibt den Wert der Testfunktion an der Stelle 0. So wie jede andere Distribution kann man auch die Delta-Distribution als Folge von Integraltermen ausdrücken. Die Dirac-Folge
δa(x)=12πa⋅e−x22a\delta_{a}(x)= \dfrac {1}{\sqrt{2\pi a}} \cdot e^{-\dfrac {x^2}{2a}}
hat den Grenzwert (vergleiche z. B. die nebenstehende Animation)
Gw(x):=lim⁡a→0δa(x)={0x≠0∞x=0 ,{\mathrm{Gw}}(x) := \lim_{a\to 0}\delta_{a}(x)=\begin{cases} 0 & x\ne 0\\ \infty & x=0 \end{cases}\,,
was zu dem verschwindenden Integral ∫RGw(x)dx=0\textstyle \int\limits_{\R}{\rm{Gw}}(x) {\rm d}x=0 führen würde. Denn das Verhalten in nur einem Punkt fällt bei Integralen gewöhnlicher Funktionen nicht ins Gewicht.

Dirac-Kamm

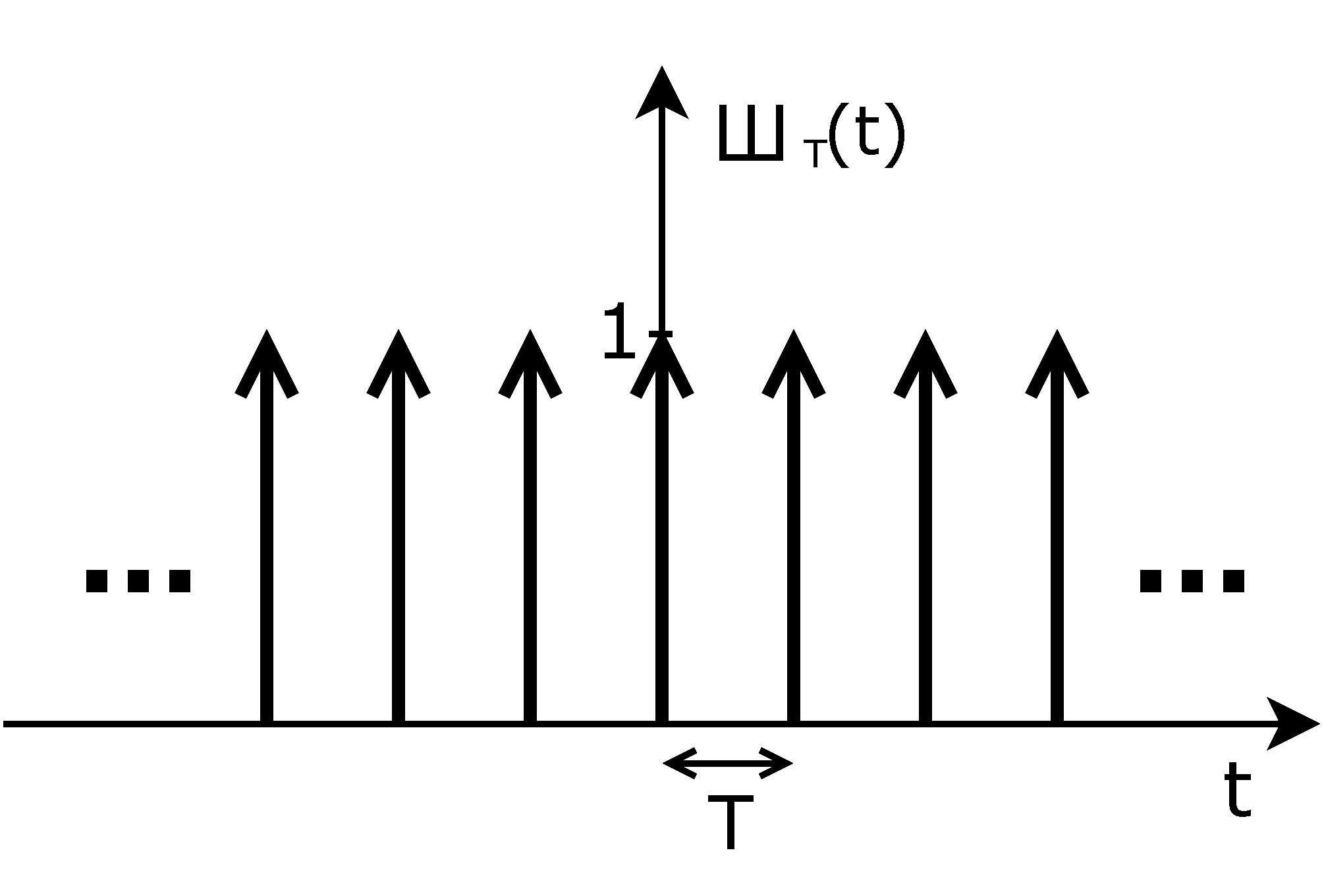
Dirac-comb.png
Der Dirac-Kamm ΔT\Delta_T ist eine periodische Distribution, die mit der diracschen Delta-Distribution eng verwandt ist. Diese Distribution ist für alle φ∈D(R)\phi \in \mathcal{D}(\R) definiert als
ΔT(φ) ⁣:=∑n∈Zφ(nT) \Delta_T(\phi) \colon= \sum\limits_{n\in\mathbb Z}\phi(nT)\,
Diese Reihe konvergiert, da die Testfunktion φ\phi kompakten Träger hat und daher nur endlich viele Summanden ungleich null sind. Eine äquivalente Definition ist
ΔT=∑n∈ZδnT,\Delta_T = \sum\limits_{n\in\mathbb Z} \delta_{n T},
wobei das Gleichheitszeichen als Gleichheit zwischen Distributionen zu verstehen ist. Die Reihe auf der rechten Seite konvergiert dann bezüglich der Schwach-*-Topologie. Auf die Konvergenz von Distributionen wird im Abschnitt Konvergenz näher eingegangen. Das in der Definition auftretende TT ist eine reelle Zahl, die man als Periode des Dirac-Kamms bezeichnet. Anschaulich ist der Dirac-Kamm also aus unendlich vielen Delta-Distributionen zusammengesetzt, die im Abstand TT zueinander stehen. Der Dirac-Kamm hat im Gegensatz zur Delta-Distribution keinen kompakten Träger. Was dies genau bedeutet, wird im Abschnitt kompakter Träger weiter unten erklärt.

Radon-Maße

Mit M(Ω)M(\Omega) wird die Menge aller Radon-Maße bezeichnet. Sei μ∈M(Ω) \mu \in M(\Omega)\, Nun kann man mittels
μ↦(φ∈D(Ω)↦∫Ωφ(x)dμ(x))\mu \mapsto \left(\phi \in \mathcal{D}(\Omega) \mapsto \int\limits_{\Omega} \phi(x) \mathrm{d} \mu(x) \right)
jedem μ\mu eine Distribution zuordnen. Auf diese Weise kann man M(Ω)M(\Omega) stetig in D′(Ω)\mathcal{D}'(\Omega) einbetten. Ein Beispiel für ein Radon-Maß ist das Dirac-Maß δ\delta. Für alle A⊂ΩA\subset \Omega ist es definiert durch
δ(A):={1 ,falls  0∈A ,0 ,sonst   \delta(A) := \begin{cases} 1\ , & \text{falls }\, 0 \in A\ , \\ 0\ , & \mathrm{sonst}\ \, \end{cases}
Identifiziert man das Dirac-Maß mit der erzeugenden Distribution
φ∈D(Ω)↦∫Ωφ(x)dδ(x)=φ(0),\phi \in \mathcal{D}(\Omega) \mapsto \int\limits_\Omega \phi(x) \mathrm{d} \delta(x) = \phi(0),
so erhält man die Delta-Distribution, falls 0∈Ω⊂Rn0 \in \Omega \subset \R^n gilt.

Cauchyscher Hauptwert von 1 / xx

Der cauchysche Hauptwert der Funktion 1x\textstyle \dfrac{1}{x} kann ebenfalls als Distribution T∈D′(R)T \in \mathcal{D}'(\R) aufgefasst werden. Für alle φ∈D(R)\phi \in \mathcal{D}(\R) setzt man
T(φ):=PV∫−∞∞φ(x)xdx T(\phi) := \text{PV} \int\limits_{-\infty}^\infty \dfrac{\phi(x)}{x} \mathrm{d} x :=lim⁡ϵ→0(∫−∞−ϵφ(x)xdx+∫ϵ∞φ(x)xdx)  := \lim_{\epsilon \to 0} \left(\int\limits_{-\infty}^{-\epsilon} \dfrac{\phi(x)}{x} \mathrm{d} x + \int\limits^{\infty}_{\epsilon} \dfrac{\phi(x)}{x} \mathrm{d} x\right)\,
Dies ist eine singuläre Distribution, da der Integralausdruck im lebesgueschen Sinn nicht definiert ist und nur als cauchyscher Hauptwert existiert. Dabei steht die Abkürzung PV für principal value.
Diese Distribution wird meist zusammen mit der Dispersionsrelation lim⁡ϵ→0+1x−iϵ = PV(1x)+iπδ(x)\textstyle \lim_{\epsilon \to 0^+}\dfrac {1}{x-i\epsilon}\,=\,{\rm{PV}} (\dfrac{1}{x})+i\pi \delta (x) benutzt, wobei alle Distributionen, insbesondere δ(φ)\delta (\phi ) und T(φ),T(\phi ), wie angegeben durch verallgemeinerte Funktionen ausgedrückt sind und ii die imaginäre Einheit bedeutet. Diese Beziehung verbindet in der linearen Antwort-Theorie Real- und Imaginärteil einer Antwortfunktion, siehe Kramers-Kronig-Beziehungen. (An dieser Stelle wird angenommen, dass die Testfunktionen φ\phi komplex sind, also ∈C\in\mathbb C, und auch die gerade angesprochenen Antwortfunktionen; aber das Argument xx soll nach wie vor reell sein, obwohl natürlich x-iϵ\epsilon komplex ist, und nicht reell.)

Oszillierendes Integral

Für alle Symbole a∈S1,0m(Ω×Rn)a \in S^m_{1,0}(\Omega \times \R^n) wird durch das oszillierende Integral I(a)(x)=∫Rnei⟨x,ξ⟩a(x,ξ)dξI(a)(x) = \int\limits_{\R^n} e^{i \langle x , \xi\rangle} a(x,\xi) \mathrm{d}\xi eine Distribution erzeugt. Diese Distribution wird zumeist durch die Integraldarstellung ∫Rn×Rnei⟨x,ξ⟩a(x,ξ)φ(x)d(x,ξ)\int\limits_{\R^n \times \R^n} e^{i \langle x , \xi\rangle} a(x,\xi) \phi(x) \mathrm{d} (x, \xi ) beschrieben. Oszillierende Integrale konvergieren im Allgemeinen jedoch nicht im lebesgueschen Sinn.
 
 

Das Buch der Natur ist mit mathematischen Symbolen geschrieben.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Distribution (Mathematik) aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Funktionalanalysis