Schwache Ableitung

Eine schwache Ableitung ermöglicht es, Funktionen eine Ableitung zuzuordnen, die nicht (stark) differenzierbar sind.
Schwache Ableitungen spielen eine große Rolle in der Theorie der partiellen Differentialgleichungen. Räume schwach differenzierbarer Funktionen sind die Sobolew-Räume.
Ein noch allgemeinerer Begriff der Ableitung ist die Distributionenableitung.

Definition für reelle Funktionen

Betrachtet man eine auf einem offenen Intervall I=]a,b[I = ]a,b[ differenzierbare Funktion ff und eine Testfunktion φ\varphi (das heißt, φ\varphi ist beliebig oft differenzierbar und besitzt einen kompakten Träger), dann gilt
∫If′(t)φ(t) dt=−∫If(t)φ′(t) dt \int\limits_I f^\prime(t) \varphi(t) \,\mathrm{d}t = - \int\limits_I f(t) \varphi^\prime(t) \,\mathrm{d}t.
Hierbei wurde die partielle Integration verwendet, wobei die Randterme wegfallen (φ(a)=0,φ(b)=0)(\varphi(a) = 0, \varphi(b) = 0).
Ist ff eine L2L^2-Funktion, dann kann, selbst wenn ff nicht differenzierbar ist (genauer: keinen differenzierbaren Vertreter in der Äquivalenzklasse besitzt), eine Funktion g∈L2(a,b)g \in L^2(a,b) existieren, die die Gleichung
∫Ig(t)φ(t) dt=−∫If(t)φ′(t) dt \int\limits_I g(t) \varphi(t) \,\mathrm{d}t = - \int\limits_I f(t) \varphi^\prime(t) \,\mathrm{d}t
für jede Testfunktion φ\varphi erfüllt. Eine solche Funktion gg heißt schwache Ableitung von ff. Man schreibt wie bei der starken Ableitung f′:=gf^\prime := g.
Die schwache Ableitung ist, wenn sie existiert, eindeutig: gäbe es zwei schwache Ableitungen g1g_1 und g2g_2, dann müsste nach der Definition
∫I(g1(t)−g2(t))φ(t) dt=0 \int\limits_I (g_1(t) - g_2(t)) \varphi(t) \,\mathrm{d}t = 0
für alle Testfunktionen φ\varphi gelten, was aber nach dem Lemma von Du Bois-Reymond g1=g2g_1 = g_2 bedeutet (im L2L^2-Sinne, d.h. fast überall), da die Testfunktionen dicht in LpL^p liegen ( für 1≤p<∞ 1 \leq p < \infty ).
Ferner stimmen bei jeder stark differenzierbaren Funktion starke und schwache Ableitung überein, so dass man von einer Verallgemeinerung des Ableitungsbegriffs sprechen kann. Im Gegensatz zur starken Ableitung ist die schwache Ableitung aber nicht punktweise, sondern nur für die ganze Funktion definiert.
Man kann statt f,f′∈L2f, f^\prime \in L^2 auch allgemeiner f,f′∈Lpf, f^\prime \in L^p für 1≤p≤∞1 \leq p \leq \infty fordern. Die Teilmenge der Funktionen aus LpL^p in der n≥1n \geq 1 schwache Ableitungen existieren ist ein sogenannter Sobolew-Raum.
Es ist zu beachten, dass sich die schwache Differenzierbarkeit immer auf die gesamte Funktion bezieht und nicht (wie die gewöhnliche Ableitung) punktweise definiert ist. Punktweise muss eine Ableitung nicht einmal existieren. Es lässt sich allerdings zeigen, dass hinreichend oft vorhandene, schwache Differenzierbarkeit auch wieder Differenzierbarkeit im üblichen Sinne (starke oder gewöhnliche Differenzierbarkeit) nach sich zieht. D.h. es gibt Einbettungen eines Sobolew-Raums mit nn schwachen Ableitungen in Räume kk-fach differenzierbarer Funktionen CkC^k mit n>k≥0n > k \ge 0.

Beispiele

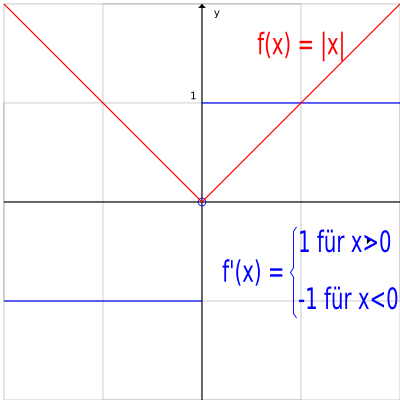
Abs_x.png
Schwache Ableitung Absolutbetrag
Die Betragsfunktion f(x)=∣x∣f(x) = |x| (vgl. Beispiel nicht differenzierbare Funktion) ist in jedem Punkt außer x=0x = 0 stark differenzierbar und besitzt daher auf ganz R\R keine starke Ableitung. Auf R∖{0}\R \setminus \{0\} ist die Funktion
f′(x)={−1:x<0+1:x>0 f^\prime(x) = \begin{cases} -1 : & x < 0\\ +1 : & x > 0 \end{cases}
die starke Ableitung von ff. Diese Funktion kann aber zu einer schwachen Ableitung der Betragsfunktion (auf ganz R\R) fortgesetzt werden, da {0}\{0\} eine Nullmenge und daher bei der Integration unbedeutend ist (man kann den Wert an der Stelle 0 beliebig setzen, wie auch auf jeder anderen Teilmenge mit dem Maß 0). Diese, auf R\R fortgesetzte Funktion, heißt Signumfunktion. Die Signumfunktion selbst ist nicht mehr schwach differenzierbar, aber man kann sie im Sinne von Distributionen ableiten.

Eigenschaften

  • Die schwache Ableitung einer differenzierbaren Funktion fällt dann im Allgemeinen mit ihrer klassischen Ableitung zusammen (wobei hier nur eine Gleichheit im L2L^2-Sinn vorliegt: zwei Funktionen sind genau dann gleich, wenn ∣∣f−g∣∣L2=0||f-g||_{L^2}=0).
  • Eine Funktion, die hinreichend oft schwach differenzierbar ist, ist auch stark differenzierbar (Einbettungssätze, siehe Sobolew-Raum).
  • Eine stetige Funktion besitzt eine schwache Ableitung, wenn sie absolutstetig ist.
Tatsächlich lassen sich in einer weiteren Verallgemeinerung auch Ableitungen gebrochener Ordnung gewinnen.

Anwendungen

Schwache Ableitungen werden systematisch untersucht in Sobolew-Räumen und zum Beispiel bei der Lösung von partiellen Differentialgleichungen verwendet.

Verallgemeinerungen der schwachen Ableitung

Schwache Ableitungen können auch für Funktionen auf höherdimensionalen Räumen definiert werden. Entsprechend kann man auch die höheren schwachen Ableitungen definieren.
Es seien Ω⊆Rn, f:Ω→R\Omega\subseteq \R^n,\, f : \Omega \rightarrow \R eine quadratisch integrierbare Funktion, das heißt, f∈L2(Ω)f \in L^2(\Omega), und α=(α1,…,αn)∈N0n\alpha = (\alpha_1, \dots, \alpha_n) \in \N_0^n ein Multiindex.
Eine Funktion gg heißt α\alpha-te schwache Ableitung von ff, falls für alle Testfunktionen φ\varphi gilt:
∫Ωg(x)φ(x) dx=(−1)∣α∣∫Ωf(x)Dαφ(x) dx\int\limits_{\Omega}g(x) \varphi(x)\, \mathrm{d}x = (-1)^{|\alpha|}\int\limits_{\Omega}f(x) D^{\alpha}\varphi(x) \,\mathrm{d}x.
Hierbei ist ∣α∣=∑i=1nαi|\alpha| = \sum\limits_{i=1}^n\alpha_i und Dαφ=∂∣α∣∂α1x1…∂αnxnφD^{\alpha}\varphi = \dfrac{\partial^{|\alpha|}}{\partial^{\alpha_1}x_1\dots \partial^{\alpha_n}x_n}\varphi.
Liegt eine Funktion f:Ω→Rmf : \Omega \rightarrow \R^m vor, so fordert man die schwache Differenzierbarkeit in jeder der mm Bildkomponenten.
Insbesondere lässt sich die Definition der schwachen Ableitung auf unbeschränkte Mengen (also ganz R\R oder Rn\R^n), Räume periodischer Funktionen oder Räume auf der Kugel oder höherdimensionalen Sphären erweitern. Auch im mehrdimensionalen Fall und bei höheren Ableitungen lassen sich Sobolew-Räume definieren.

Literatur

  • Dirk Werner: Funktionalanalysis, Springer-Verlag, Berlin, ISBN 978-3-540-72533-6
  • Lawrence Evans: Partial Differential Equations, American Mathematical Society, ISBN 0-8218-0772-2
 
 

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Schwache Ableitung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analysis