Approximation der Delta-Distribution

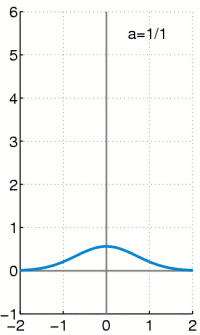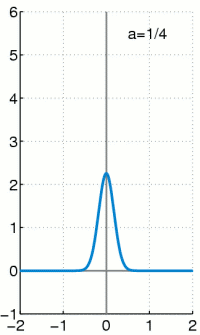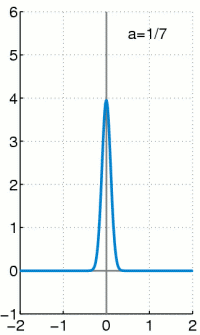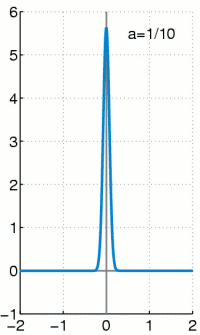
Dichte einer zentrierten Normalverteilung $\delta_{a}(x)=\dfrac {1}{\sqrt{2\pi a}} \cdot e^{-\dfrac {x^2}{2a}}$.
Für $a\to 0$ wird die Funktion immer höher und schmaler, der Flächeninhalt bleibt jedoch unverändert 1. (Unterbrechung mit Esc-Taste.)

Dirac-Folgen

1. für alle $x \in \R^n$ und alle $k \in \N$ die Bedingung $\delta_{k}(x)\geq 0\,,$
2. für alle $k \in \N$ die Identität $\int\limits_{\R^n}\delta_{k}(x)\,\mathrm{d}x=1$ und
3. für alle $\delta > 0$ die Gleichheit $\lim_{t \to \infty} \int\limits_{\R^n \setminus B_\delta (0)} \delta_{k}(x) \mathrm{d} x = 0$

Bemerkungen

$\delta_k(f) := \langle\delta_{k},f\rangle := \int\limits_{\R^n}\delta_{k}(x)\, f(x)\,\mathrm{d}x$

$\lim_{k\to \infty} \delta_k(f) = \lim_{k\to \infty} \langle\delta_{k},f\rangle=f(0)=\langle\delta,f\rangle$

Beispiele für Dirac-Folgen

• Glockenfunktionen (Normalverteilungen)

$\delta_{\epsilon}(x)=\dfrac{1}{\sqrt{2\pi\varepsilon}}\,\exp\left(-\dfrac{x^{2}}{2\varepsilon}\right)$

Die angegebenen Funktionen besitzen ein sehr schmales und sehr hohes Maximum bei x=0, die Breite ist ~ $\sqrt{\epsilon}\to 0$ und die Höhe ~ $1/\sqrt{\epsilon}\to\infty$. Der Flächeninhalt unter der Funktion ist aber immer 1, für alle $\epsilon$.

• Lorentzkurven

$\delta_{\epsilon}(x)=\dfrac{1}{\pi}\dfrac{\epsilon}{x^{2}+\epsilon^{2}}$

• Fresnel-Darstellung

$\delta_{\epsilon}(x)=\dfrac{1}{\sqrt{i\pi\epsilon}}\,\exp\left(\dfrac{ix^{2}}{\epsilon}\right)$

die man sich vorstellen kann als eine Linie, die auf einen Zylinder gewickelt ist, und deren Wicklungen durch das $x^2$ immer enger werden; die Grundfläche (in $x$-$y$-Ausrichtung) des Zylinders wird aus dem Imaginär- und Realteil der Funktion gebildet, die Funktion entwickelt sich dann in $z$-Richtung.

• Rechteckfunktion

$\delta_{\epsilon}(x)=\dfrac{\textrm{rect}(x/\epsilon)}{\epsilon}=\begin{cases} \dfrac{1}{\epsilon} & \ |x|\leq\dfrac{\epsilon}{2}\\ 0 & \ \text{sonst}\end{cases}$

• Dreiecksfunktion

$\delta_{\epsilon}(x)=\begin{cases} \dfrac{\epsilon+x}{\epsilon^{2}} & \ -\epsilon\leq x\leq0\\ \dfrac{\epsilon-x}{\epsilon^{2}} & \ 0<x\leq\epsilon\\ 0 & \ \text{sonst}\end{cases}$

• Exponentialfunktion um Ursprung abfallend

$\delta_{\epsilon}(x)=\dfrac{1}{2\epsilon}\exp\left(-\dfrac{|x|}{\epsilon}\right)$

Weitere Beispiele

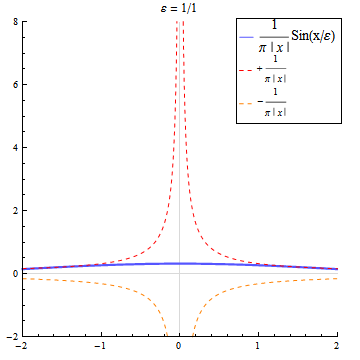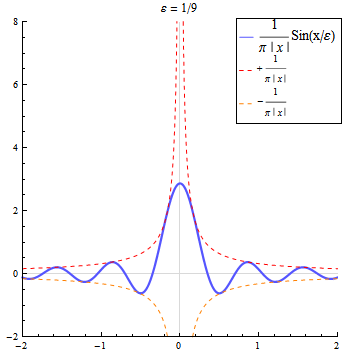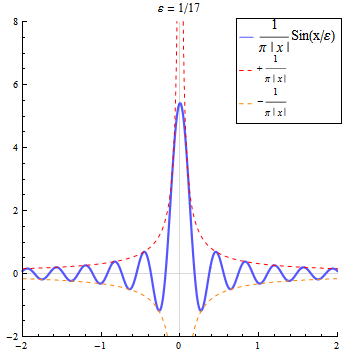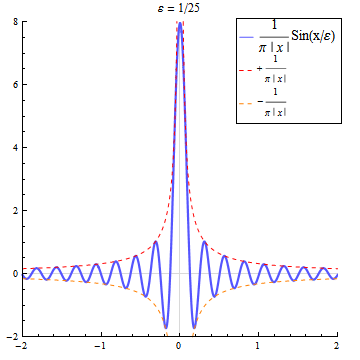
Approximation durch die Sincfunktion

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Beispiele

• Delta-Distribution
  • Approximation
  • Eigenschaften
  • Mehrdimensionale Delta-Distributionen