Potenzen und Wurzeln komplexer Zahlen

Aus der Eulerschen Formel können wir eine allgemeine Formel für die Potenzierung von komplexen Zahlen ableiten, die Moivresche Formel oder Formel von Moivre:

Hierbei ist $r\in\dom R$ eine beliebige reelle Zahl und $\phi=\arg(z)$ das Argument. Wenn $r$ nicht ganzzahlig ist, ist die Potenz oder Wurzel nicht eindeutig, daher das $2k\pi$ Glied. Die Lösung mit dem kleinsten positiven $\phi$ wird Hauptwert genannt.

(Für einen strengen Existenzbeweis siehe Satz A4KD)

$\sqrtN 3 {-8}={(-4)}^{\frac 1 3}$

$=|-8|^{\frac 1 3}\e^{\frac 1 3 \, \i(\pi+2k\pi)}$ (Das Argument für eine negative Zahl ist $\pi$)

$=\sqrtN 3 8 \e^{\i \cdot \braceNT{\frac \pi 3 + \frac {2k\pi} 3}}$

$=2 \braceNT{\cos\braceNT{\dfrac \pi 3 + \dfrac {2k\pi} 3} +\i\sin\braceNT{\dfrac \pi 3 + \dfrac {2k\pi} 3}}$ (mit der Eulerschen Formel)

Neben dem Hauptwert mit dem Argument $\dfrac \pi 3$ gibt es weitere Lösungen für die beiden Argumente $\pi$ und $\dfrac 5 3 \pi$. Die dazugehörigen Lösungen sind:

$2\braceNT{\cos\braceNT{\dfrac \pi 3}+\i \sin \braceNT{\dfrac \pi 3}}=1+ \sqrt 3 \i$

$2(\cos \pi +\i\sin \pi)=-2$

$2\braceNT{\cos\braceNT{\dfrac 5 3 \pi}+\i \sin \braceNT{\dfrac 5 3 \pi}}=1- \sqrt 3 \i$

Für eine komplexe Zahl $z$ sind die beiden Lösungen von $\sqrt{z}$ ununterscheidbar. Es gibt also nicht wie im Reellen eine positive Wurzel, die man im Allgemeinen mit der Wurzel identifiziert.

Sei $z=x+\i y$, dann ergibt sich für die beiden Wurzeln im Komplexen die folgende Zerlegung in Realteil und Imaginärteil:

Dabei steht $\sgn(y)$ für das Vorzeichen von $y$.

Sei $w=u+\i v$ und $w^2=z$. Also $u^2-v^2+2uv\i=x+\i y$, was die beiden Gleichungen ergibt. Dieses Gleichungssystem muss nach $u,v$ aufgelöst werden.

Es ist $|z|=|w^2|$ $=|w|^2=u^2+v^2$, also $|z|+x=u^2+v^2+u^2-v^2=2u^2$ und $|z|-x=u^2+v^2-(u^2-v^2)=2v^2$, womit sich $u=\pm\sqrt{\dfrac{|z| + x}{2}}$ und $v=\pm\sqrt{\dfrac{|z| - x}{2}}$. Die Probe für $x$ ergibt $x=u^2-v^2$ $=\dfrac{|z| + x}{2}-\dfrac{|z| - x}{2}=x$ und für $y$ erhält man $y=2uv$ $=2\cdot \sqrt{\dfrac{|z| + x}{2}}\, \cdot\sqrt{\dfrac{|z| - x}{2}}$ $=\sqrt{(|z| + x)(|z| - x)}$ $=\sqrt{|z|^2-x^2}=\sqrt{y^2}$. Diese Gleichung gilt genau dann, wenn das Vorzeichen der Wurzel mit dem Vorzeichen von $y$ übereinstimmt. Daher kommt der $\sgn$-Term in Formel (1).
Ist $z$ in trigonometrischer Darstellung gegeben, dann ergibt sich nach Anwendung der Moivreschen Formel für die Quadratwurzel die Darstellung

wobei $n$ die Werte $0$ oder $1$ annehmen kann.

An Darstellung (2) können wir ablesen, dass der Betrag der Wurzel der Wurzel aus dem Betrag der komplexen Zahl entspricht. Das Argument wird halbiert und die andere Lösungen ergibt sich geometrisch in der Gaußschen Zahlenebene durch Spiegelung am Ursprung. Wie im Reellen ist mit $w$ auch $-w$ Lösung von $\sqrt z$.

Quadratwurzeln aus $z = -1+\i\sqrt{3}$

Anwenden von Formel (1): $w_1 = \sqrt{\dfrac{2-1} 2}+\i \sqrt{\dfrac{2+1} 2}$ $=\sqrt{\dfrac{1} 2}+\i \sqrt{\dfrac{3} 2}$ $=\dfrac 1 2\sqrt 2 (1+\i\sqrt 3 )$.

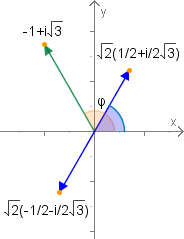
Die zweite Wurzel erhält man durch Vorzeichenumkehr:

$w_2 = -w_1 = \dfrac 1 2\sqrt{2} \cdot \braceNT{ -1 - \i \cdot \sqrt{3} }$.