Komplexer Logarithmus

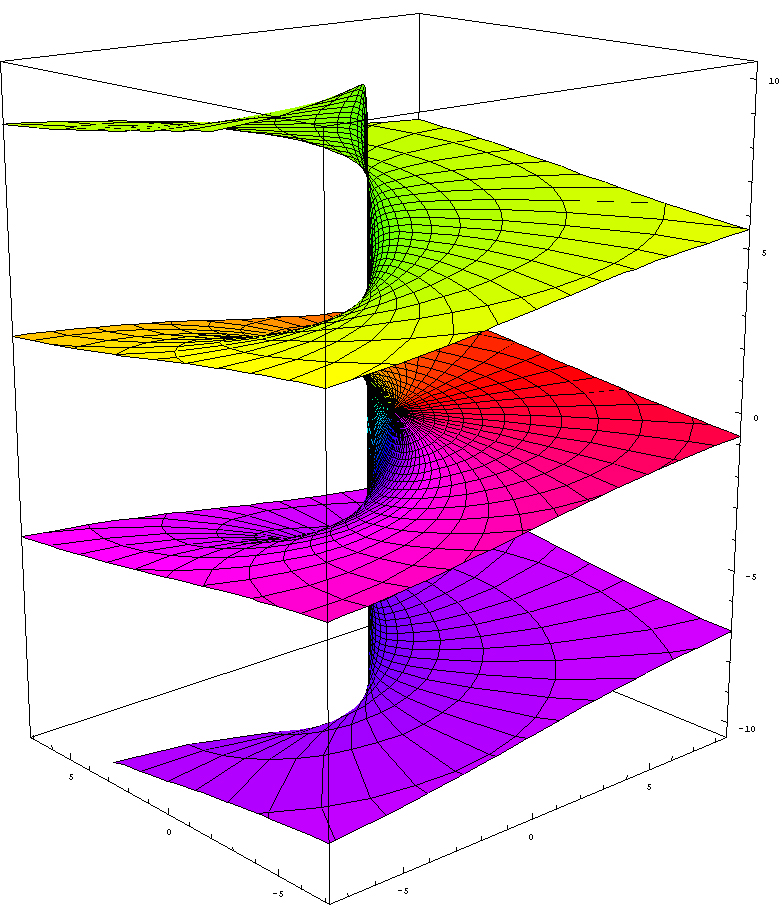
Riemann_surface_log.jpg
Riemannsche Fläche der komplexen Logarithmus-Funktion, die Blätter entstehen aufgrund der Mehrdeutigkeit
Analog zur reellen Definition heißt jede komplexe Zahl ww, welche die Gleichung
ew=ze^w = z
erfüllt, ein natürlicher Logarithmus von zz. Dies ist im Unterschied zum reellen Logarithmus jedoch nicht eindeutig, da
e2kπi=1,k∈Ze^{2k\pi i} = 1, \quad k \in \Z
gilt, siehe dazu auch Eulersche Identität. Hat man also einen Logarithmus ww von zz gefunden, so ist damit auch
w′=  ⁣w+2kπiw' =\,\! w + 2k\pi i
ein Logarithmus von zz, da gilt:
ew′=ew+2kπi=ew⋅e2kπi=ew⋅1=ze^{w'} = e^{w + 2k\pi i} = e^w \cdot e^{2k\pi i} = e^w \cdot 1 = z
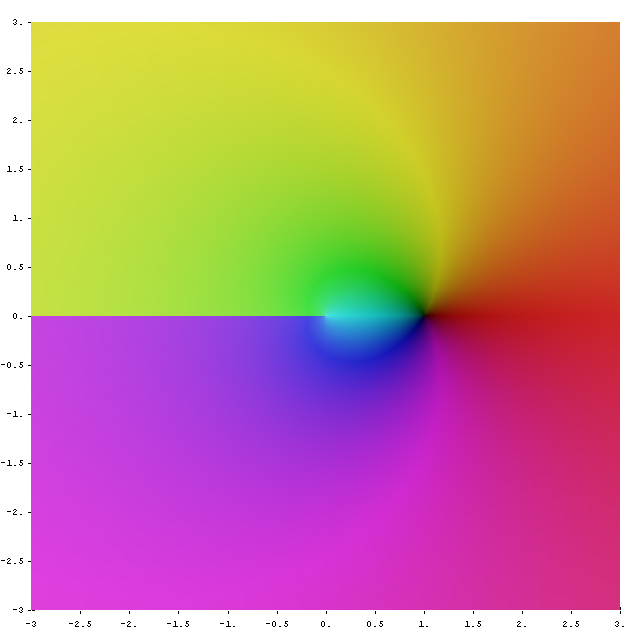
Complex_log.jpg
Hauptwert des Logarithmus =ln⁡z= \ln z
Um Eindeutigkeit zu erreichen, schränkt man ww auf einen Streifen in der komplexen Zahlenebene ein. Man kann z. B. den Streifen
{w∈C:−π<Im⁡ w≤π}\left\{w \in \mathbb C: -\pi < \operatorname{Im}\,w \leq \pi \right\}
verwenden. Eine komplexe Zahl aus diesem Streifen heißt Hauptwert des Logarithmus und man schreibt w=ln⁡zw = \ln z. Stellt man zz in Polarkoordinaten dar, so erhält man eine einfache Darstellung des k-ten Zweigs der Logarithmusfunktion:
w=ln⁡∣z∣+i(arg⁡z+2kπ),k∈Z w = \ln |z| + i\left(\arg z + 2k\pi\right), \quad k\in\Z\,
Für k=0k = 0 hat man dann den Hauptzweig des Logarithmus:
ln⁡z=ln⁡∣z∣+iarg⁡z\ln z = \ln|z| + i\arg z
ln⁡\ln ist nicht stetig auf C∖{0}\mathbb C\setminus\{0\}. Entfernt man jedoch die negative reelle Achse, so ist ln⁡\ln auf dem Gebiet
C∖{x∈R:x≤0}\mathbb C\setminus\{x \in \R: x\leq 0\}
stetig und sogar holomorph. Allgemeiner gilt dies für alle einfach zusammenhängenden, offenen Teilmengen von C∖{0}\mathbb C\setminus\{0\}.
Mit dem Hauptzweig des komplexen Logarithmus kann man den Logarithmus von negativen, reellen Zahlen bestimmen:
ln⁡(−x)=ln⁡∣−x∣+iarg⁡(−x)=ln⁡x+iπ,x∈R+ \ln(-x) = \ln|-x| + i\arg(-x) = \ln x + i\pi, \quad x\in\R^+\,
Man muss jedoch beachten, dass im Komplexen die Rechenregeln für Logarithmen nicht immer gelten, sondern nur noch modulo 2πi2 \pi i. Es gilt dann beispielsweise nicht notwendig
ln⁡x+ln⁡y=ln⁡(x⋅y),\ln x + \ln y = \ln(x \cdot y),
wegen
ln⁡(−1)+ln⁡(−1)=2πi≠0=ln⁡1=ln⁡((−1)⋅(−1)) \ln(-1) + \ln(-1) = 2\pi i\neq 0 = \ln 1 = \ln((-1) \cdot (-1))\,
Und auch die Gleichung
y⋅ln⁡x=ln⁡xyy \cdot \ln x = \ln{x^y}
ist nicht notwendig erfüllt, was durch das Gegenbeispiel
2πiln⁡e=2πi≠0=ln⁡1=ln⁡(e2πi)2\pi i \ln e = 2\pi i\neq 0 = \ln 1 = \ln(e^{2\pi i})
verdeutlicht wird.
 
 

Beispiele

1) ln⁡(1)=2kπi⁡\ln(1)=2k\pi\i
2) ln⁡(−1)=ln⁡∣−1∣+πi⁡+2kπi⁡=(2k+1)πi⁡\ln(-1)=\ln|-1|+\pi\i+2k\pi\i=(2k+1)\pi\i
3) ln⁡(i⁡)=ln⁡∣i⁡∣+π2i⁡+2kπi⁡\ln(\i)=\ln|\i|+\dfrac \pi 2 \i+2k\pi\i =(12+2k)πi⁡=\braceNT{\dfrac 1 2 +2k}\pi\i
4) i⁡i⁡=i⁡ln⁡i⁡=i⁡(12+2k)πi⁡=−(12+2k)π\i^\i=\i\ln \i=\i \braceNT{\dfrac 1 2 +2k}\pi\i=-\braceNT{\dfrac 1 2 +2k}\pi
Erstaunlich an diesem Beispiel ist, dass das Ergebnis eine reelle Zahl ist.

Man darf nicht das, was uns unwahrscheinlich und unnatürlich erscheint, mit dem verwechseln, was absolut unmöglich ist.

Carl Friedrich Gauß

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Logarithmus aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Funktionentheorie