Gaußsche Zahlenebene
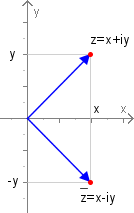
Die komplexen Zahlen kann man sich in einem -Koordinatensystem veranschaulichen, dieses heißt Gaußsche Zahlenebene oder auch komplexe Zahlenebene. Auf der -Achse wird der Realteil abgetragen und sie wird als reelle Achse bezeichnet. Auf der -Achse wird der Imaginärteil abgetragen und sie heißt dementsprechend imaginäre Achse.
Damit kann man eine komplexe Zahl als Vektor in der euklidischen Ebene auffassen. Der konjugierten Zahl entspricht der an der reellen Achse (x-Achse) gespiegelte Vektor.
Die Länge des Vektors ist dann der Betrag der komplexen Zahl. Alle komplexen Zahlen mit dem gleichen Betrag liegen somit auf einem Kreis um den Ursprung, dessen Radius genau dem Betrag entspricht.
Veranschaulichung von Addition und Subtraktion
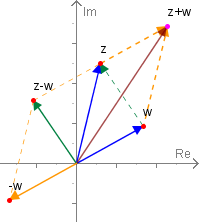
Die Addition zweier komplexer Zahlen und entspricht der Vektoraddition in der Gaußschen Zahlenebene und die Subtraktion komplexer Zahlen lässt sich als Vektorsubtraktion veranschaulichen.
Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.
Richard Feynman
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе