Trigonometrische Form komplexer Zahlen

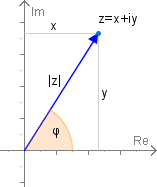
TrigDarstellung1.png
Aus der Veranschaulichung einer komplexen Zahl z=x+i⁡yz=x+\i y in der Gaußschen Zahlenebene können wir sofort die trigonometrische Darstellung ableiten:
z=∣z∣(cos⁡φ+i⁡sin⁡φ)z=|z|(\cos\phi +\i\sin\phi)
Dabei ist φ\phi der Winkel zwischen reeller Achse und Ortsvektor der komplexen Zahl; er heißt auch Argument der komplexen Zahl zz und wird mit arg⁡(z)=φ\arg(z)=\phi bezeichnet.
Das Argument φ\phi kann man aus tan⁡φ=yx\tan \phi= \dfrac y x bestimmen. Dabei ist auf die korrekten Quadranten zu achten.
 
 

Multiplikation und Division

Die Addition komplexer Zahlen lässt sich in der trigonometrischen Darstellung nicht trivial ausführen, dafür gibt es für die Multiplikation eine einfache Formel. Haben wir z=∣z∣(cos⁡φ+i⁡sin⁡φ)z=|z|(\cos\phi +\i\sin\phi) und w=∣w∣(cos⁡ψ+i⁡sin⁡ψ)w=|w|(\cos\psi +\i\sin\psi) so gilt:
z⋅w=∣z∣∣w∣(cos⁡φ+i⁡sin⁡φ)(cos⁡ψ+i⁡sin⁡ψ)z\cdot w=|z||w|(\cos\phi +\i\sin\phi)(\cos\psi +\i\sin\psi) =∣zw∣(cos⁡φcos⁡ψ−sin⁡φsin⁡ψ=|zw|(\cos\phi\cos\psi-\sin\phi\sin\psi +i⁡(cos⁡φsin⁡ψ+sin⁡φcos⁡ψ))+\i(\cos\phi\sin\psi+\sin\phi\cos\psi))
=∣zw∣(cos⁡(φ+ψ)+i⁡sin⁡(φ+ψ))=|zw|(\cos(\phi+\psi)+\i\sin(\phi+\psi)) (Additionstheoreme Satz 5220A)
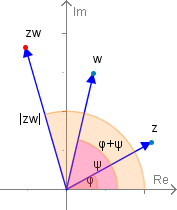
TrigDarMul.png
Damit hat das Produkt z⋅wz\cdot w den Betrag des Produktes und als Argument die Summe der Argumente.
Mit z‾=∣z‾∣(cos⁡φ−i⁡sin⁡φ)\overline z=|\overline z|(\cos\phi -\i\sin\phi) =∣z∣(cos⁡(−φ)+i⁡sin⁡(−φ))=|z|(\cos(-\phi) +\i\sin(-\phi)) finden wir auch die trigonometrische Darstellung für einen Quotienten.
zw=z⋅w‾w⋅w‾\dfrac z w=\dfrac {z\cdot \overline w}{w\cdot \overline w} =∣z∣∣w∣∣w∣2(cos⁡φ+i⁡sin⁡φ)(cos⁡ψ−i⁡sin⁡ψ)=\dfrac {|z||w|}{|w|^2}(\cos\phi +\i\sin\phi)(\cos\psi -\i\sin\psi) =∣z∣∣w∣(cos⁡(φ−ψ)+i⁡sin⁡(φ−ψ))=\dfrac {|z|}{|w|} (\cos(\phi-\psi)+\i\sin(\phi-\psi)).

Das ist ein Mittel, das Paradies nicht zu verfehlen: auf der einen Seite einen Mathematiker, auf der anderen einen Jesuiten; mit dieser Begleitung muß man seinen Weg machen, oder man macht ihn niemals.

Friedrich der Große

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Funktionentheorie