Komplexe Funktionen
Eine Abbildung mit heißt eine komplexe Funktion oder komplexwertige Funktion. Ordnet jedem ein zu, so schreibt man
Die Menge heißt Definitionsbereich der Funktion . Die Menge aller Funktionswerte heißt der Wertebereich der Funktion.
Zerlegen wir nun [!Argument] und Funktionswert in ihren jeweiligen Realteil und Imaginärteil:
- und ,
- und .
Darstellung komplexer Funktionen
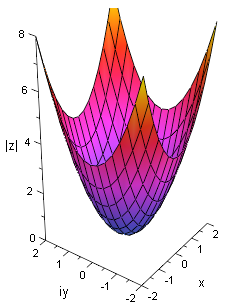
Da wir es bei Funktionen einer komplexen Veränderlichen mit vier reellen Variablen zu tun haben, ist eine bequeme Veranschaulichung, wie wir sie von reellen Funktionen mit zwei oder auch drei Variablen kennen, nicht möglich.
Bei einer Funktion von zwei reellen unabhängigen Variablen lässt sich ein Funktionswert als "Höhe" eines Punktes über der -Ebene darstellen, und die Gesamtheit der Funktionswerte bildet eine Fläche (ein "Gelände") im Raum. Bei Funktionen einer komplexen Variablen dagegen sind die Funktionswerte ebenfalls komplexe Zahlen, um obiges Schema anwenden zu können müssen wir sie auf reelle Werte herunterbrechen.
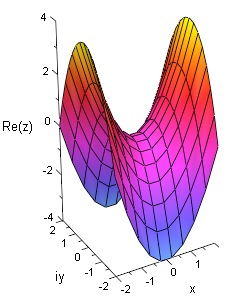
Dazu bestehen prinzipiell 3 Möglichkeiten. Wir tragen auf der Höhenachse:
- den Absolutbetrag
- den Realteil oder
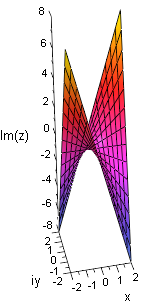
- den Imaginärteil ab.
Am gängigsten ist es, den Betrag abzutragen.
In den nebenstehenden Grafiken sind alle drei Varianten für die komplexe Funktion
dargestellt.
Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.
Karl Menger
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе