Symmetriegruppen

Bewegungen, die Figuren in sich selbst überführen, werden Symmetrien genannt. Diese Symmetrien bilden bzgl. der Hintereinanderausführung eine Gruppe.

Beispiele

Rechteck

Nehmen wir als Beispiel ein Rechteck.

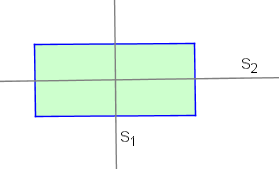
Neben der Identischen Abbildung

I

, die das Rechteck unverändert lässt, gibt es eine Drehung

D

um 180°, die es in sich selbst überführt. Außerdem sind noch zwei Spiegelungen möglich

S_1

und

S_2

an den entsprechenden Achsen.

Die Gruppentafel veranschaulicht, wie diese Symmetrien zusammenhängen und beschreibt damit die Symmetriegruppe des Rechtecks.

$I$	$D$	$S_1$	$S_2$
$D$	$I$	$S_2$	$S_1$
$S_1$	$S_2$	$I$	$D$
$S_2$	$S_1$	$D$	$I$

Diese Gruppe wird als Kleinsche Vierergruppe bezeichnet und man benutzt das Symbol

\bm{D_2}

. Sie ist kommutativ.

Gleichseitiges Dreieck (Beispiel C7JG)

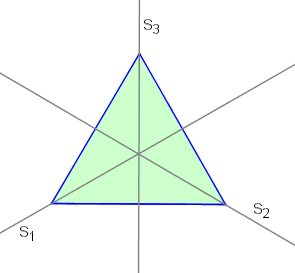
Für ein gleichseitiges Dreieck erhält man eine 6-elementige Symmetriegruppe bestehend aus 3 Drehungen (wir fassen die Identische Abbildung als Drehung um 0° auf) und drei Spiegelungen.

$D_{0°}$	$D_{120°}$	$D_{240°}$	$S_1$	$S_2$	$S_3$
$D_{120°}$	$D_{240°}$	$D_{0°}$	$S_2$	$S_3$	$S_1$
$D_{240°}$	$D_{0°}$	$D_{120°}$	$S_3$	$S_1$	$S_2$
$S_1$	$S_3$	$S_2$	$D_{0°}$	$D_{240°}$	$D_{120°}$
$S_2$	$S_1$	$S_3$	$D_{120°}$	$D_{0°}$	$D_{240°}$
$S_3$	$S_2$	$S_1$	$D_{240°}$	$D_{120°}$	$D_{0°}$

Diese Gruppe ist isomorph zur symmetrischen Gruppe

\bm{S_3}

Ähnlich kann man die Symmetriegruppen aller regelmäßigen n-Ecke konstruieren. Im Grenzfall erhält man die Symmetriegruppe des Kreises, die natürlich nicht mehr endlich ist.

In Gruppentafeln gilt allgemein: Jedes Gruppenelement kommt in jeder Zeile und jeder Spalte genau einmal vor.

Die beste von allen Sprachen der Welt ist eine künstliche Sprache, eine ziemlich gedrängte Sprache, die Sprache der Mathematik.

N. I. Lobatschewski

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе

Datenschutzerklärung

Algebra

Gleichungen
Gruppen
- Halbgruppen und Monoide
- Beispiele
- Gruppentafel
- Symmetriegruppen
- Kommutative Gruppen
- Untergruppen
- Homomorphismus
- Spezielle Gruppen
- Isomorphietypen
Ringe und Körper
Algebren
Polynome
Ordnungstheorie