Bernsteinpolynome

Die Bernsteinpolynome sind eine Familie reeller Polynome mit ganzzahligen Koeffizienten. Sie haben ihren Ursprung in der Approximationstheorie. Mit ihrer Hilfe konnte ihr Entdecker Sergei Natanovich Bernstein im Jahre 1911 einen konstruktiven Beweis für den Approximationssatz von Weierstraß angeben. Ende der 1950er Jahre gab es erste Versuche, auf Bernsteinpolynomen basierende Methoden im Design von Kurven und Flächen einzusetzen.

Definition

Für n∈N0n\in\N_0 heißen die reellen Polynome
Bi,n:R→RB_{i,n}:\R \to \R, t↦(ni) ti (1−t)n−it \mapsto \chooseNT{n }{ i}\, t^i\, (1-t)^{n-i}
(mit 0≤i≤n0\leq i\leq n) die Bernsteinpolynome vom Grad nn.
Durch lineare Transformation (Abbildung des Intervalls [0,1][0,1] auf ein beliebiges Intervall [a,b][a,b]) erhält man die verallgemeinerten Bernsteinpolynome
Bi,n[a,b]:R→RB_{i,n}^{[a,b]}:\R \to \R, t↦1(b−a)n(ni)(t−a)i (b−t)n−i t \mapsto \dfrac{1}{(b-a)^n} \chooseNT{n }{ i} (t-a)^i\, (b-t)^{n-i}.
Dabei bezeichnet
(ni)=n!i!(n−i)!\chooseNT{n }{ i} = \dfrac{n!}{i! (n-i)!}
den Binomialkoeffizienten.
Beachte: Diese Definition erklärt eigentlich die den Polynomen zugehörigen Polynomfunktionen.

Beispiel

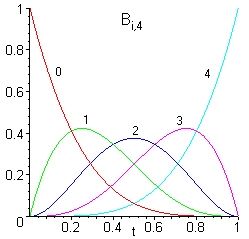
Bernsteinpolynom.png
Die Bernsteinpolynome Bi,4B_{i,4}
Die folgende [!Abbildung] zeigt die Bernsteinpolynome Bi,4B_{i,4}, 0≤i≤n0\leq i\leq n vom Grad 44:
Bernsteinpolynome sind die Grundlage von Bézierkurven, die bei der computergestützten Beschreibung von Kurven, Flächen und Schriften eine wichtige Rolle spielen.

Eigenschaften

Die Bernsteinpolynome bezüglich des Intervalls [0,1][0,1] haben folgende Eigenschaften:
  • Basiseigenschaft: Die Bernsteinpolynome {Bi,n:0≤i≤n}\{B_{i,n}:0\leq i\leq n\} sind linear unabhängig und bilden eine Basis von Πn\Pi_n, dem Raum der Polynome vom Grad kleiner oder gleich n.
  • Positivität:
    • Bi,n(t)>0B_{i,n}(t) > 0 für alle t∈(0,1)t \in (0,1).
  • Extrema: Bi,nB_{i,n} besitzt im Intervall [0,1][0,1] genau ein (absolutes) Maximum. Es befindet sich an der Stelle t=int = \dfrac{i}{n}. Für i∈{0,n}i\in\{0,n\} erhält man insbesondere
B0,n(0)=Bn,n(1)=1B_{0,n}(0) = B_{n,n}(1) = 1
  • Zerlegung der Eins (auch Partition der Eins):
    • ∑i=0nBi,n(t)=∑i=0n(ni)ti(1−t)n−i=1\sum\limits_{i=0}^n B_{i,n}(t) = \sum\limits_{i=0}^n\chooseNT{n }{ i} t^i (1-t)^{n-i} = 1
(Ergibt sich mit Hilfe des binomischen Lehrsatzes aus (t+(1−t))n(t+(1-t))^n.)
  • Symmetrie:
    • Bi,n(t)=Bn−i,n(1−t)B_{i,n}(t) = B_{n-i,n}(1-t)
  • Rekursionsformel:
    • Bi,n(t)=(1−t)⋅Bi,n−1(t)+t⋅Bi−1,n−1(t)B_{i,n}(t) = (1-t) \cdot B_{i,n-1}(t) + t \cdot B_{i-1,n-1}(t), mit der Definition
    Bi,n:=0B_{i,n} := 0 für i<0i < 0 oder i>ni > n
    B0,0:=1 B_{0,0} := 1
  • Gradanhebung:
    • Bi,n(t)=i+1n+1⋅Bi+1,n+1(t)+n+1−in+1⋅Bi,n+1(t)B_{i,n}(t) = \dfrac{i+1}{n+1} \cdot B_{i+1,n+1}(t) + \dfrac{n+1-i}{n+1} \cdot B_{i,n+1}(t)
  • Ableitungen:
    • Bi,n′(t)=n[Bi−1,n−1(t)−Bi,n−1(t)]B'_{i,n}(t) = n \left[ B_{i-1,n-1}(t) - B_{i,n-1}(t) \right], mit der Definition
    B−1,n−1,Bn,n−1:=0B_{-1,n-1}, B_{n,n-1} := 0

Approximation mit Bernsteinpolynomen

Für jede Funktion f:[0,1]→Rf: [0,1] \to \R heißt das durch Bn(f)(t)=∑i=0nBi,n(t)⋅f(in) B_n(f)(t) = \sum\limits_{i=0}^n B_{i,n}(t)\cdot f\left(\dfrac{i}{n}\right) definierte Polynom Bn(f)B_n(f) das "nn-te Bernsteinpolynom der Funktion ff".
Wenn ff eine stetige Funktion ist, dann konvergiert die Folge der Bernsteinpolynome von ff gleichmäßig gegen ff.

Literatur

  • Bernstein, S.N., Démonstration du Théorème de Weierstrass fondée sûr le calcul dés Probabilités, Commun. Soc. Math. Khrakow, Vol. 12, No. 2, pp. 1-2, 1912.
 
 

Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Bernsteinpolynom aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerische Verfahren