Bézierkurven

Kubische Bézierkurve

Definition

$C(t) := C_0^n(t)$

$C(t)_i^j := \begin{cases} (1-t)C_i^{j-1}(t) + tC_{i+1}^{j-1}(t), & j>0 \\ P_i, & \text{sonst } \end{cases}$

$C(t) = \sum\limits_{i=0}^n \binom n i t^i (1-t)^{n-i} P_i$$= \sum\limits_{i=0}^n B_{i,n}(t) P_i$

Eigenschaften

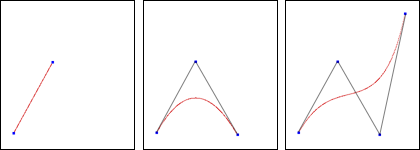
Bezier Kurven (rot) der Grade 1, 2 und 3 und zugehörige Kontrollpolygone (grau). Von links nach rechts wurde jeweils ein Kontrollpunkt (blau) hinzugefügt. Man erkennt wie die Kurve bei Einfügen/Verändern eines Kontrollpunkts "oszilliert", d.h. sich komplett verändert.

• Die Kurve liegt innerhalb der konvexen Hülle des Kontrollpolygons. Dies folgt daraus, dass die Bernsteinpolynome vom Grad $n$ eine Zerlegung der Eins sind: $1 = \sum\limits_{i=0}^n B_{i,n}(t)$ $t \in [0,1]$
• Die Kurve geht genau durch die Endpunkte $P_0$ und $P_n$:

$C(0) = \sum\limits_{i=0}^n \binom n i 0^i(1-0)^{n-i} P_i = P_0$

$C(1) = P_n$

• Die Tangenten in den Endpunkten sind:

$C'(0) =n \cdot (P_1 - P_0)$,

$C'(1) = n \cdot (P_n - P_{n-1})$.

• Eine Gerade schneidet eine Bézierkurve höchstens so oft, wie sie ihr Kontrollpolygon schneidet (die Kurve hat eine beschränkte Schwankung).
• Eine affine Transformation (Verschiebung, Skalierung, Rotation, Scherung) kann auf die Bézierkurve durch Transformation des Kontrollpolygons angewendet werden ("affine Invarianz").
• Liegen alle Kontrollpunkte auf einer Geraden, so wird die Bézierkurve zu einer Strecke (Vorteil gegenüber der Polynominterpolation).
• Der Einfluss eines Kontrollpunktes auf die Kurve ist global. D.h.: Verschiebt man einen Punkte, verändert sich die gesamte Kurve. Daher verwendet man in der Praxis meist Splines, zusammengesetzte Kurven festen Grades, die stetig ineinander übergehen.

$C(u, v) = \sum\limits_{i=0}^n \sum\limits_{j=0}^m P_{i,j} B_{i,n}(u) B_{j,m}(v)$,

Anwendung

Beispiele

Lineare Bézierkurven (n=1)

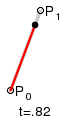
Konstruktion einer linearen Bézierkurve

$C(t) = \sum\limits_{i=0}^1 t^i (1-t)^{1-i} P_i$$=\ (1-t)P_0 + t P_1$, $t \in [0,1]$.

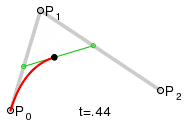
Quadratische Bézierkurven (n=2)

$C(t) = \sum\limits_{i=0}^2 t^i (1-t)^{1-i} P_i$$=\ (1 - t)^{2}P_0 + 2t(1 - t)P_1 + t^{2}P_2$, $t \in [0,1]$.

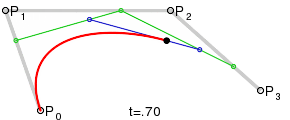
Kubische Bézierkurven (n=3)

$C(t) \$$= \ \sum\limits_{i=0}^3 \binom 3 i t^i (1-t)^{3-i}$$= \ (1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3$$= \ \underbrace{(t^3 t^2 t 1)}_\text{Monome} \underbrace{\begin{pmatrix} -1 & 3 & -3 & 1 \\ 3 & -6& 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix}}_\text{Basismatrix} \underbrace{\begin{pmatrix} P_0 \\ P_1 \\ P_2 \\ P_3 \end{pmatrix}}_\text{Geometrievektor}$, $t \in [0,1]$.

Literatur

• Gerald Farin: Curves and Surfaces for CAGD. A practical guide. 5. Aufl. Academic Press, San Diego 2002, ISBN 1-55860-737-4
• David Salomon: Curves and Surfaces for Computer Graphics. Springer Science+Business Media, Inc., 2006, ISBN 0-387-24196-5

Das Buch der Natur ist mit mathematischen Symbolen geschrieben.

Galileo Galilei

Approximation

• Satz von Stone-Weierstraß
• Bernsteinpolynome
  • Bézierkurven