Übersicht über Interpolationsverfahren
Lineare Interpolation
Die von Isaac Newton begründete lineare Interpolation ist am einfachsten und wird wohl in der Praxis am häufigsten benutzt. Hier werden zwei gegebene Datenpunkte und durch eine Strecke verbunden. Es gilt:
.
Dies entspricht einer Konvexkombination der Endpunkte und . Detaillierte Erläuterungen unter Allgemeine lineare Interpolation.
Höhergradige Polynome
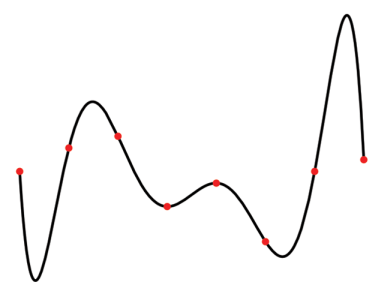
Interpolationspolynom 7. Grades
Der Fundamentalsatz der Algebra garantiert, dass man zu paarweise verschiedenen Datenpunkten genau ein Interpolationspolynom -ten Grades finden kann. Die Bestimmung der Koeffizienten erfordert die Lösung eines linearen Gleichungssystems. Man erhält das Interpolationspolynom z.B. mit Hilfe der Formel von Lagrange:
Weitere Verfahren zur Polynominterpolation siehe dort.
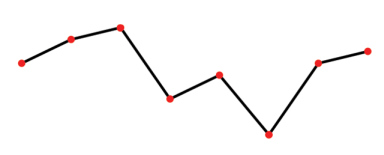
Stückweise lineare Interpolation
Stückweise Interpolation
Da Polynome mit zunehmendem Grad immer instabiler werden (d.h. sie schwingen stark zwischen den Interpolationspunkten), werden in der Praxis Polynome mit Grad > 5 kaum eingesetzt. Stattdessen interpoliert man einen großen Datensatz stückweise. Im Fall der linearen Interpolation wäre das ein Polygonzug, bei Polynomen vom Grad 2 oder 3 spricht man üblicherweise von Spline-Interpolation. Bei abschnittsweise definierten Interpolanten ist die Frage der Stetigkeit und Differenzierbarkeit an den Stützstellen von großer Bedeutung.

Hermite-Interpolation
Sind zusätzlich zu den Stützstellen auch noch die -Ableitungen zu interpolieren, so spricht man von einem Hermite-Interpolationsproblem. Die Lösung dieses Problems lässt sich analog zum Lagrange-Verfahren ebenfalls in geschlossener Form angeben.
Trigonometrische Interpolation
Wählt man als Ansatzfunktion ein trigonometrisches Polynom, so erhält man eine trigonometrische Interpolation. Die Interpolationsformel
,
entspricht einer Fourier-Entwicklung der unbekannten Interpolanten. Die Fourier-Koeffizienten und berechnen sich zu
und .
Dabei wird angenommen, dass die Stützstellen im Intervall äquidistant verteilt sowie außerhalb dieses Intervalls periodisch sind. Die Koeffizienten können effizient mit Hilfe der schnellen Fourier-Transformation berechnet werden.
Logarithmische Interpolation
Vermutet bzw. weiß man, dass den Daten eine logarithmische Funktion zugrunde liegt, so empfiehlt sich dieses Verfahren. Dabei werden zwei bekannte Datenpunkte und durch eine logarithmische Kurve verbunden. Es gilt:
Oder anders formuliert:
Beispiel: -Test
Jede mathematische Formel in einem Buch halbiert die Verkaufszahl dieses Buches.
Stephen Hawking
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Interpolation
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе