Verfahren der konjugierten Gradienten

Das CG-Verfahren (von engl. c\bm{c}onjugate g\bm{g}radients oder auch Verfahren der konjugierten Gradienten) ist eine effiziente numerische Methode zur Lösung von großen, symmetrischen, positiv definiten Gleichungssystemen der Form Ax=bAx=b. Es gehört zur Klasse der Krylow-Unterraum-Verfahren. Das Verfahren konvergiert nach spätestens mm Schritten. Insbesondere ist es aber als iteratives Verfahren interessant, da der Fehler monoton fällt.
 
 

Idee des CG-Verfahrens

Die Idee des CG-Verfahrens besteht darin, dass das Maximieren von
E(x):=⟨b,x⟩−12⟨Ax,x⟩E(x):=\langle b,x\rangle-\dfrac12\langle Ax,x\rangle
äquivalent zum Lösen von Ax=bAx=b ist.
Der Gradient von EE an der Stelle x(k)x^{(k)} ist gerade g(k)=b−Ax(k)g^{(k)}=b-Ax^{(k)} und somit bei großen, dünn besetzten Matrizen schnell zu berechnen. Die Idee des CG-Verfahrens ist es nun, anstelle in Richtung g(k)g^{(k)} in eine andere Richtung d(k)d^{(k)} die Funktion EE zu maximieren. Die Richtungen d(k)d^{(k)} sind dabei alle AA-konjugiert, d.h. es gilt
⟨Ad(i),d(j)⟩=0∀i≠j\langle Ad^{(i)},d^{(j)}\rangle=0\qquad\forall i\neq j.
Weiter realisieren alle x(k)x^{(k)} das Maximum von EE in dem affinen Raum
Vk:=x(0)+span⁡({d(1),…,d(k)})V_k:=x^{(0)}+\operatorname{span}\left(\{d^{(1)},\ldots,d^{(k)}\}\right).
Dabei handelt es sich also um den Vektorraum, der durch die Vektoren d(1),…,d(k)d^{(1)},\ldots,d^{(k)} aufgespannt und um x(0)x^{(0)} verschoben wird.
Da die Vektoren d(k)d^{(k)} alle AA-konjugiert sind, ist die Dimension von VkV_k gerade kk. Ist also AA eine m×mm\times m-Matrix, so terminiert das Verfahren nach spätestens mm Schritten, falls korrekt gerechnet wird. Numerische Fehler können durch weitere Iterationen eliminiert werden. Hierzu betrachtet man den Gradienten g(k)g^{(k)}, der den numerischen Fehler, d.h. das Residuum angibt. Unterschreitet die Norm dieses Residuums einen gewissen Schwellenwert, wird das Verfahren abgebrochen.
Das Verfahren baut sukzessive eine orthogonale Basis für den Rm\mathbb R^m auf und minimiert in die jeweilige Richtung bestmöglich.

CG-Verfahren ohne Vorkonditionierung

Zunächst wählt man ein x(0)∈Rmx^{(0)}\in\mathbb{R}^m beliebig und berechnet:
g(0)=b−Ax(0)g^{(0)} = b - A x^{(0)}
d(0)=−g(0)d^{(0)} = -g^{(0)}
Für k=0,1,…k = 0,1,\dots setzt man:
Finde von x(k)x^{(k)} in Richtung d(k)d^{(k)} das Minimum x(k+1)x^{(k+1)} und aktualisiere den Gradienten bzw. das Residuum
α(k)=g(k)T g(k)d(k)T A d(k)\alpha^{(k)}=\dfrac{g^{(k)^T}\,g^{(k)}}{d^{(k)^T}\,A\,d^{(k)}}
x(k+1)=x(k)−α(k) d(k)x^{(k+1)}=x^{(k)}-\alpha^{(k)}\,d^{(k)}
g(k+1)=g(k)+α(k) A d(k)g^{(k+1)}=g^{(k)}+\alpha^{(k)}\,A\,d^{(k)}
Korrigiere die Suchrichtung d(k+1)d^{(k+1)} mit Hilfe von d(k)d^{(k)} und g(k+1)g^{(k+1)}
βk=g(k+1)Tg(k+1)g(k)Tg(k)\beta_k=\dfrac{g^{(k+1)^T} g^{(k+1)}}{g^{(k)^T} g^{(k)}}
d(k+1)=−g(k+1)+βkd(k)d^{(k+1)}=-g^{(k+1)}+\beta_k d^{(k)}
bis das Residuum in der Norm kleiner als eine Toleranz ist (∥g(k+1)∥<tol)(\|g^{(k+1)}\|<\text{tol}).

CG-Verfahren mit symmetrischer Vorkonditionierung (PCG-Verfahren)

Die Konvergenz des CG-Verfahren ist nur bei symmetrischen positiv definiten Matrizen gesichert. Dies muss ein Vorkonditionierer berücksichtigen. Bei einer symmetrischen Vorkonditionierung wird das Gleichungssystem Ax=bAx=b mithilfe einer Vorkonditionierer-Matrix C=KKT≈A−1C=KK^T\approx A^{-1} zu KTAKy=KTbK^TAKy=K^Tb mit y=K−1xy=K^{-1}x transformiert, und darauf das CG-Verfahren angewandt.
Die Matrix KTAKK^TAK ist symmetrisch, da A symmetrisch ist. Sie ist ferner positiv definit, da nach dem Trägheitssatz von Sylvester AA und KTAKK^TAK die gleichen Anzahlen positiver und negativer Eigenwerte besitzen.
Das resultierende Verfahren ist das sogenannte PCG-Verfahren (von engl. P\bm{P}reconditioned C\bm Conjugate G\bm{G}radient):
Zunächst wählt man ein x(0)∈Rmx^{(0)}\in\mathbb{R}^m beliebig und berechnet:
g(0)=b−Ax(0)g^{(0)} = b - A x^{(0)}
h(0)=Cg(0)h^{(0)} = C g^{(0)}
d(0)=−h(0)d^{(0)} = -h^{(0)}
Für k=0,1,…k = 0,1,\dots setzt man:
Finde von x(k)x^{(k)} in Richtung d(k)d^{(k)} das Minimum x(k+1)x^{(k+1)} und aktualisiere Gradienten und vorkonditionierten Gradienten
αk=⟨g(k),h(k)⟩⟨d(k),Ad(k)⟩\alpha_k=\dfrac{\langle g^{(k)}, h^{(k)}\rangle}{\langle d^{(k)}, A d^{(k)}\rangle}
x(k+1)=x(k)−αkd(k)x^{(k+1)}=x^{(k)}-\alpha_k d^{(k)}
g(k+1)=g(k)+αkAd(k)g^{(k+1)}=g^{(k)}+\alpha_k A d^{(k)} (Residuum)
h(k+1)=Cg(k+1)h^{(k+1)}=C g^{(k+1)}
Korrigiere die Suchrichtung d(k+1)d^{(k+1)}
βk=⟨g(k+1),h(k+1)⟩⟨g(k),h(k)⟩\beta_k=\dfrac{\langle g^{(k+1)}, h^{(k+1)}\rangle}{\langle g^{(k)}, h^{(k)}\rangle}
d(k+1)=−h(k+1)+βkd(k)d^{(k+1)}=-h^{(k+1)}+\beta_k d^{(k)}
bis das Residuum in der Norm kleiner als eine Toleranz ist (∥g(k+1)∥<tol)(\|g^{(k+1)}\|<\text{tol}).
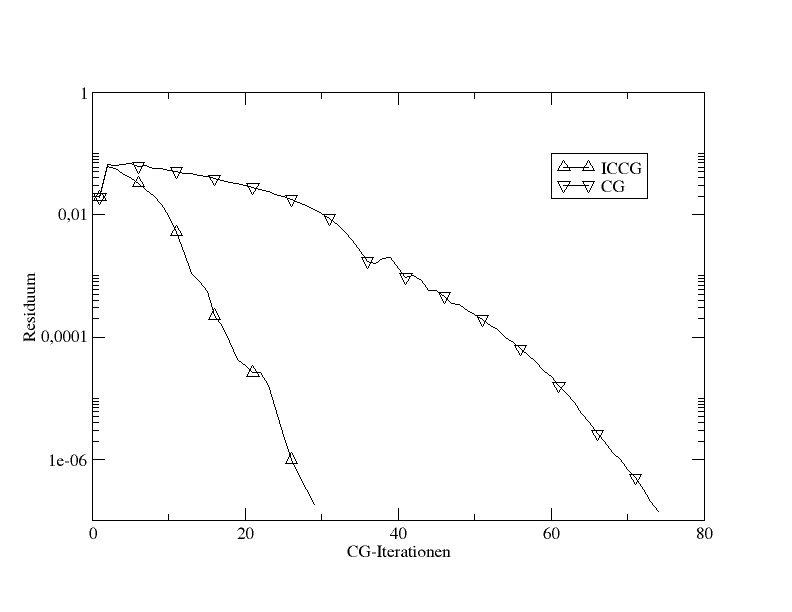
ICCG-CG-comparison.png
Vergleich von ICCG mit CG anhand der 2D-Poisson-Gleichung
Ein häufiger Vorkonditionierer im Zusammenhang mit CG ist die unvollständige Cholesky-Zerlegung. Diese [!Kombination] wird auch als ICCG bezeichnet und wurde in den 1970ern von Meijerink und van der Vorst eingeführt.
Zwei weitere für das PCG-Verfahren zulässige Vorkonditionierer sind der Jacobi-Vorkonditionierer C=D−1C=D^{-1}, wobei DD die Hauptdiagonale von AA ist, und der SSOR-Vorkonditionierer C=(12−ω(1ωD+L)(1ωD)−1(1ωD+L)T)−1C=(\dfrac{1}{2-\omega}(\dfrac{1}{\omega}D+L)(\dfrac{1}{\omega}D)^{-1}(\dfrac{1}{\omega}D+L)^T)^{-1} mit ω∈(0, 2)\omega \in (0, \,2), wobei DD die Hauptdiagonale und LL die strikte untere Dreiecksmatrix von AA ist.

Konvergenzrate CG-Verfahrens

Man kann zeigen, dass die Konvergenz des CG-Algorithmus
∥xk−x∥A≤2κ(A)−1κ(A)+1∥xk−1−x∥A\|x_k-x\|_A \le 2\dfrac{\sqrt{\kappa(A)}-1}{\sqrt{\kappa(A)}+1}\|x_{k-1}-x\|_A
ist. Hierbei ist κ(A)\kappa(A) die Kondition der Matrix AA, sowie ∥⋅∥A=∥A⋅∥2\|\cdot\|_A = \|A \cdot\|_2 die AA-Norm.
(κ(A)−1)(\sqrt{\kappa(A)}-1) ist nicht negativ, da AA symmetrisch und positiv definit ist. Damit ist die Kondition
κ(A)=λmax(A)λmin(A)\kappa(A) = \dfrac{\lambda_{max}(A)}{\lambda_{min}(A)}
und es gilt
0<λmin(A)≤λmax(A)⇒1≤λmaxλmin 0<\lambda_{min}(A) \le \lambda_{max}(A) \Rightarrow 1 \le \dfrac{\lambda_{max}}{\lambda_{min}}\,

Literatur

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel CG-Verfahren aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Lineare Gleichungssysteme