Logarithmische Spirale

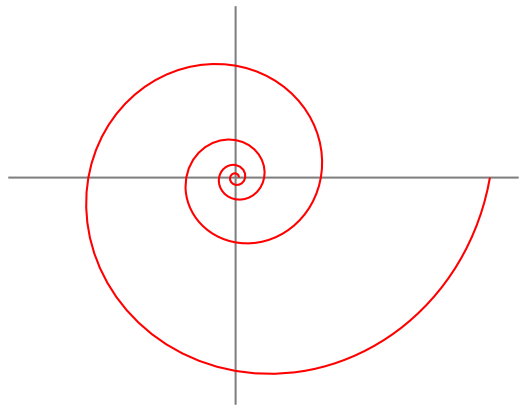
Logarithmic_spiral.png
Logarithmische Spirale, rechtsdrehend
Die logarithmische Spirale ist eine Spirale, die mit jeder Umdrehung den Abstand von ihrem Mittelpunkt, dem Pol, um den gleichen Faktor vergrößert. In umgekehrter Drehrichtung schlingt sich die Kurve mit abnehmendem Radius immer enger um den Pol. Jede Gerade durch den Pol schneidet die logarithmische Spirale stets unter dem gleichen Winkel. Wegen dieser Eigenschaft spricht man auch von einer gleichwinkligen Spirale.
 
 

Mathematische Darstellung

Am leichtesten lässt sich eine logarithmische Spirale in Polarkoordinaten (r,φ)(r, \varphi) angeben:
r(φ)=aekφa,k∈R, k≠0r(\varphi) = a e^{k\varphi} \quad a, k \in \mathbb R,\, k \neq 0
mit k=k = const. als Steigung der Spirale, und dem Steigungswinkel α, tan⁡α=k\alpha,\, \tan \alpha = k
In kartesischen Koordinaten ergibt sich:
x(φ)=r(φ)cos⁡φ=aekφcos⁡φ,x(\varphi) = r(\varphi) \cos{\varphi} = a e^{k \varphi} \cos{\varphi},
y(φ)=r(φ)sin⁡φ=aekφsin⁡φ y(\varphi) = r(\varphi) \sin{\varphi} = a e^{k \varphi} \sin{\varphi}\,
Namensgebend ist die implizite Darstellung:
φ=1kln⁡(ra) \varphi = \dfrac {1}{k} \ln \left( \dfrac {r}{a} \right)\,
ra\dfrac {r}{a} lässt sich hierbei als normierter Radius verstehen.
In der komplexen Ebene lässt sich jede logarithmische Spirale sogar noch einfacher darstellen:
w(t)=ztz∈C,t∈R,∣z∣≠1,Im(z)≠0,w(t) = z^t \quad z \in \mathbb C, t \in \mathbb R, \left|z\right| \ne 1, \mathrm{Im}(z) \ne 0,
denn
zt=etln⁡z=et(ln⁡∣z∣+iarg⁡z)=∣z∣teitarg⁡z=∣z∣t(cos⁡(targ⁡z)+isin⁡(targ⁡z)) z^t = e^{t\ln z} = e^{t \left(\ln |z| + i\arg z\right)} = |z|^t e^{it\arg z} = |z|^t \left(\cos \left(t\arg z\right) + i \sin \left(t\arg z\right)\right)\,

Eigenschaften

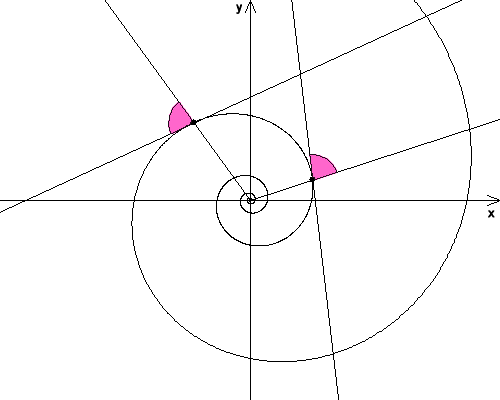
Logarithmische_SpiraleP.png
Logarithmische Spirale: alle durch den Pol gehenden Geraden schneiden die Kurve unter dem gleichen Tangentenwinkel
Die logarithmische Spirale hat eine Reihe einzigartiger Eigenschaften, weshalb sie von einem ihrer größten Liebhaber, Jakob Bernoulli, auch als spira mirabilis ("wundersame Spirale") bezeichnet wurde:
  • alle durch den Pol gehenden Geraden schneiden die Kurve - also ihre Tangenten - unter dem gleichen Tangentenwinkel tan⁡αˉ=1k\tan \bar \alpha = \dfrac {1}{k} bzw. αˉ=π2−α\bar \alpha = \dfrac {\pi}{2} - \alpha (siehe Abbildung)
  • die Spirale umkreist den Ursprung unendlich oft, ohne ihn zu erreichen (asymptotischer Punkt)
  • obwohl unendlich viele Drehungen bis zum Erreichen des Pols benötigt werden, ist die Länge der Kurve von jedem Kurvenpunkt bis zum Pol endlich
  • mit jeder Windung wächst der Radius um einen konstanten Faktor:
r(φ+2π)=aek(φ+2π)=aek⋅2πekφ=(e2π)kr(φ)r ( \varphi +2 \pi) = a e^{k( \varphi +2 \pi)} = a e^{k \cdot 2\pi} e^{k\varphi} = (e^{2\pi})^k r ( \varphi)
mit e2πe^{2\pi} ≈ 535,5 in einer Potenz der Steigung kk (daher ergeben nur relativ flache Spiralen mit kk ≪ 1 "hübsche" Schnecken). Diese Eigenschaft unterscheidet alle logarithmischen Spiralen von den [!archimedischen=Archimedische Spirale], die sich bei jeder Windung um eine Konstante ausdehnen (ihre Steigung nimmt dabei ab)
  • die logarithmische Spirale ist - in Verallgemeinerung der obigen Herleitung - selbstähnlich (invariant) gegenüber einer zentrischen Streckung um den Faktor ekγe^{k \gamma} bei gleichzeitiger Drehung um den Winkel γ\gamma
Das gilt für die konstant wachsende Archimedesspirale nicht: Darum scheinen rotierende Archimedesspiralen "nach außen" zu wandern, aber logarithmische perspektivisch auf den Beobachter zuzukommen.
  • die Kurve ist ihre eigene Evolute
  • die Kurve ist ihre eigene Brennlinie (Kaustik)
  • die Kurve ist ihre eigene Fußpunktkurve
  • eine Inversion der Kurve (r↦1r)(r \mapsto \dfrac 1 r) führt zu Drehung und Spiegelung der Kurve an der yy-Achse (für a=1a = 1 nur zur Spiegelung); aus einer linksdrehenden logarithmischen Spirale wird eine rechtsdrehende und umgekehrt
  • alle Spiralen gleicher Steigung sind ähnlich
  • Für k→0 {k \to 0}\ nähert sich die Spirale immer mehr einem Kreis des Radius aa an, der die Kurvengleichung für k=0k = 0 (Schnittwinkel 90 Grad) erfüllt. Dass der Kreis ein Spezialfall der logarithmischen Spirale ist, ist insbesondere in der Kugelgeometrie bedeutend.

Formeln

Formeln zur Logarithmischen Spirale
Funktion r(φ)=a⋅ek⋅φr(\varphi)=a\cdot e^{k\cdot\varphi}
Steigung k=drdφ=cot⁡αk =\dfrac{\mathrm dr}{\mathrm d\varphi}=\cot\alpha
Krümmungsradius ρ=r⋅1+k2\rho=r\cdot\sqrt{1+k^2}
Bogenelement ds=1k⋅1+k2 drds=\dfrac{1}{k}\cdot\sqrt{1+k^2}\ dr
Flächenelement dA=12⋅ek⋅φ dφdA=\dfrac{1}{2}\cdot e^{k\cdot\varphi}\ d\varphi

Religion und Mathematik sind nur verschiedene Ausdrucksformen derselben göttlichen Exaktheit.

Kardinal Michael Faulhaber

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Logarithmische Spirale aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene Kurven