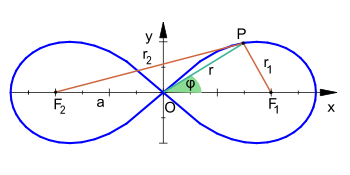
Die Lemniskate
Seien
F 1 F_1 F 1 und
F 2 F_2 F 2 zwei
Punkte , die den Abstand
2 a 2a 2 a zueinander haben. Dann ist die
Lemniskate diejenige
ebene Kurve , bei der für jeden
Punkt P P P der Kurve gilt: das Produkt der Abstände
r 1 = F 1 P ‾ r_1=\overlineI{F_1P} r 1 = F 1 P und
r 2 = F 2 P ‾ r_2=\overlineI{F_2P} r 2 = F 2 P hat den Wert
a 2 a^2 a 2 , also:
r 1 ⋅ r 2 = a 2 r_1\cdot r_2=a^2 r 1 ⋅ r 2 = a 2 .
(1) Formel 15W8 (Gleichung der Lemniskate)
Herleitung
r 1 2 = r 2 + a 2 − 2 a r ⋅ cos φ r_1^2=r^2+a^2-2ar\cdot \cos\phi r 1 2 = r 2 + a 2 − 2 a r ⋅ cos φ ,
und im
Dreieck △ F 2 O P \triangle F_2OP △ F 2 O P :
r 2 2 = r 2 + a 2 − 2 a r ⋅ cos ( π − φ ) r_2^2=r^2+a^2-2ar\cdot \cos(\pi-\phi) r 2 2 = r 2 + a 2 − 2 a r ⋅ cos ( π − φ ) = r 2 + a 2 + 2 a r ⋅ cos φ =r^2+a^2+2ar\cdot \cos\phi = r 2 + a 2 + 2 a r ⋅ cos φ .
a 4 = r 1 2 r 2 2 a^4=r_1^2r_2^2 a 4 = r 1 2 r 2 2 = ( r 2 + a 2 − 2 a r ⋅ cos φ ) ( r 2 + a 2 + 2 a r ⋅ cos φ ) =(r^2+a^2-2ar\cdot \cos\phi)(r^2+a^2+2ar\cdot \cos\phi) = ( r 2 + a 2 − 2 a r ⋅ cos φ ) ( r 2 + a 2 + 2 a r ⋅ cos φ ) = ( r 2 + a 2 ) 2 − 4 a 2 r 2 cos 2 φ =(r^2+a^2)^2-4a^2r^2\cos^2\phi = ( r 2 + a 2 ) 2 − 4 a 2 r 2 cos 2 φ ⟹ a 4 = r 4 + 2 a 2 r 2 + a 4 − 4 a 2 r 2 cos 2 φ \implies a^4=r^4+2a^2r^2+a^4-4a^2r^2\cos^2\phi ⟹ a 4 = r 4 + 2 a 2 r 2 + a 4 − 4 a 2 r 2 cos 2 φ ⟹ 0 = r 2 ( r 2 + 2 a 2 − 4 a 2 cos 2 φ ) \implies 0=r^2(r^2+2a^2-4a^2\cos^2\phi) ⟹ 0 = r 2 ( r 2 + 2 a 2 − 4 a 2 cos 2 φ ) ⟹ 0 = r 2 + 2 a 2 ( 1 − 2 cos 2 φ ) \implies 0=r^2+2a^2(1-2\cos^2\phi) ⟹ 0 = r 2 + 2 a 2 ( 1 − 2 cos 2 φ ) ⟹ 0 = r 2 + 2 a 2 ( − cos 2 φ ) \implies 0=r^2+2a^2(-\cos2\phi) ⟹ 0 = r 2 + 2 a 2 ( − cos 2 φ ) (
Satz 5316D )
⟹ r 2 = 2 a 2 cos 2 φ \implies r^2=2a^2\cos2\phi ⟹ r 2 = 2 a 2 cos 2 φ Damit haben wir die gesuchte Darstellung der Lemniskate in
Polarkoordinaten gefunden. Damit die Gleichung erfüllt ist, muss
cos 2 φ ≥ 0 \cos2\phi\geq 0 cos 2 φ ≥ 0 gelten. Dies ist der Fall für
φ ∈ [ 0 , π 4 ] ∪ [ 3 π 4 , 5 π 4 ] ∪ [ 7 π 4 , 2 π ] \phi\in\ntxbraceL{0,\dfrac \pi 4}\cup\ntxbraceL{\dfrac {3\pi} 4,\dfrac {5\pi} 4}\cup\ntxbraceL{\dfrac {7\pi} 4,2\pi} φ ∈ [ 0 , 4 π ] ∪ [ 4 3 π , 4 5 π ] ∪ [ 4 7 π , 2 π ] .
Um zu den
kartesischen Koordinaten überzugehen benutzen wir die Beziehung
cos 2 φ = cos 2 φ − sin 2 φ \cos 2\phi=\cos^2\phi-\sin^2\phi cos 2 φ = cos 2 φ − sin 2 φ (
Satz 5220A ) und
Formel 15VP . Damit ergibt sich
x 2 + y 2 = 2 a 2 ( cos 2 φ − sin 2 φ ) = 2 a 2 ( x 2 r 2 − y 2 r 2 ) x^2+y^2=2a^2(\cos^2\phi-\sin^2\phi)=2a^2\braceNT{\dfrac {x^2}{r^2}-\dfrac {y^2}{r^2}} x 2 + y 2 = 2 a 2 ( cos 2 φ − sin 2 φ ) = 2 a 2 ( r 2 x 2 − r 2 y 2 ) , woraus wir
( x 2 + y 2 ) 2 = 2 a 2 ( x 2 − y 2 ) (x^2+y^2)^2=2a^2(x^2-y^2) ( x 2 + y 2 ) 2 = 2 a 2 ( x 2 − y 2 ) erhalten.
□ \qed □ Die Lemniskate überschneidet sich im Ursprung,
r r r nimmt den Wert
0 0 0 für
φ = π 4 , 3 π 4 , 5 π 4 , 7 π 4 \phi=\dfrac \pi 4,\dfrac {3\pi} 4,\dfrac {5\pi} 4,\dfrac {7\pi} 4 φ = 4 π , 4 3 π , 4 5 π , 4 7 π . Um den
Winkel der
Tangenten in diesem
Punkt zu bestimmen berechnen wir zuerst die
Ableitungen :
x ˙ = a 2 ⋅ − 4 sin 2 φ 2 cos 2 φ ⋅ cos φ − a 2 cos 2 φ ⋅ sin φ \dot x=\dfrac a 2\cdot \dfrac {\uminus 4\sin 2\phi}{\sqrt{2\cos 2\phi}}\cdot \cos \phi-a\sqrt{2\cos 2\phi}\cdot\sin\phi x ˙ = 2 a ⋅ 2 cos 2 φ − 4 sin 2 φ ⋅ cos φ − a 2 cos 2 φ ⋅ sin φ = − a ( 2 sin 2 φ ⋅ cos φ 2 cos 2 φ + 2 cos 2 φ ⋅ sin φ 2 cos 2 φ ) =-a\braceNT{\dfrac{2\sin 2\phi\cdot\cos \phi}{\sqrt{2\cos 2\phi}}+\dfrac{2\cos 2\phi\cdot\sin\phi} {\sqrt{2\cos 2\phi}}} = − a ( 2 cos 2 φ 2 sin 2 φ ⋅ cos φ + 2 cos 2 φ 2 cos 2 φ ⋅ sin φ ) = − 2 a sin 3 φ 2 cos 2 φ =-2a\dfrac {\sin 3\phi}{\sqrt{2\cos 2\phi}} = − 2 a 2 cos 2 φ sin 3 φ y ˙ = a 2 ⋅ − 4 sin 2 φ 2 cos 2 φ ⋅ sin φ − a 2 cos 2 φ ⋅ cos φ \dot y=\dfrac a 2\cdot \dfrac {\uminus 4\sin 2\phi}{\sqrt{2\cos 2\phi}}\cdot \sin \phi-a\sqrt{2\cos 2\phi}\cdot\cos\phi y ˙ = 2 a ⋅ 2 cos 2 φ − 4 sin 2 φ ⋅ sin φ − a 2 cos 2 φ ⋅ cos φ = a ( − 2 sin 2 φ ⋅ sin φ 2 cos 2 φ + 2 cos 2 φ ⋅ cos φ 2 cos 2 φ ) =a\braceNT{-\dfrac{2\sin 2\phi\cdot\sin \phi}{\sqrt{2\cos 2\phi}}+\dfrac{2\cos 2\phi\cdot\cos\phi} {\sqrt{2\cos 2\phi}}} = a ( − 2 cos 2 φ 2 sin 2 φ ⋅ sin φ + 2 cos 2 φ 2 cos 2 φ ⋅ cos φ ) = 2 a cos 3 φ 2 cos 2 φ =2a\dfrac {\cos 3\phi}{\sqrt{2\cos 2\phi}} = 2 a 2 cos 2 φ cos 3 φ Also
y ′ = − cot 3 φ y'=-\cot 3\phi y ′ = − cot 3 φ . Für
φ = π 4 \phi=\dfrac \pi 4 φ = 4 π ergibt sich dann
y ′ = 1 y'=1 y ′ = 1 , eine
Gerade mit dem
Anstieg 1 und dem
Winkel 45°.
Ein Mathematiker ist eine Maschine, die Kaffee in Theoreme verwandelt.
Paul Erdös
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе