Tangentialvektor

Für eine ebene Kurve in Parameterdarstellung (x(t),y(t))(x(t), y(t)) bestimmt man die Ableitungen nach dem Parameter tt zu:
x˙(t):=d⁡x(t)d⁡t\dot x(t):=\dfrac {\d x(t)}{\d t}
y˙(t):=d⁡y(t)d⁡t\dot y(t):=\dfrac {\d y(t)}{\d t}
Es besteht folgender Zusammenhang zur Ableitung der Funktion:
y′=d⁡yd⁡x= d⁡yd⁡t⋅d⁡td⁡x=y˙x˙y'=\dfrac {\d y}{\d x}=\ \dfrac {\d y}{\d t}\cdot \dfrac {\d t} {\d x}=\dfrac {\dot y} {\dot x}
Die Vektor, dessen Komponenten die Ableitung sind, (x˙(t),y˙(t))(\dot x(t),\dot y(t)) beschreibt einen Tangentialvektor oder Tangentenvektor an die Kurve. In jedem Punkt der ebenen Kurven wird durch ihn die Richtung der Tangente an die Kurve in diesem Punkt bestimmt.
Deutet man den Parameter tt als Zeit, so entspricht der Tangentialvektor einem Geschwindigkeitsvektor.

Beispiel

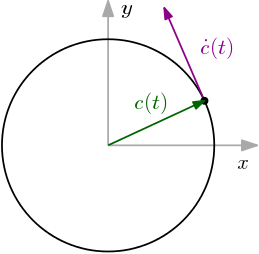
TangenteKreis.png
Durch c(t)=(cos⁡t,sin⁡t)c(t)=(\cos t,\sin t) wird ein Einheitskreis gegeben. Die Ableitung ist c˙(t)=(−sin⁡t,cos⁡t)\dot c(t)=(-\sin t, \cos t). Berechnen wir jetzt das Skalarprodukt zwischen Tangentialvektor und Ortvektor, so ergibt sich
⟨c(t),c˙(t)⟩=0\spo c(t),\dot c(t)\spc= 0.
Damit stehen die Vektoren senkrecht aufeinander, wie es beim Kreis zu erwarten war.
 
 

Gott existiert, weil die Mathematik widerspruchsfrei ist, und der Teufel existiert, weil wir das nicht beweisen können.

Andre Weil

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Kurventheorie