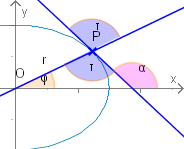
Der Tangentialvektor in Polarkoordinaten

Ist eine ebene Kurve in Polarkoordinaten als r=r(φ)r=r(\phi) gegeben und bezeichnen wir mit r˙=d⁡rd⁡φ\dot r=\dfrac{\d r}{\d \phi}, so erhalten wir die Komponenten des Tangentialvektors über die Beziehungen x=r⋅cos⁡φx=r\cdot \cos\phi und y=r⋅sin⁡φy=r\cdot \sin\phi (Formel 15VQ). Es gilt unter Benutzung der Kettenregel:
x˙=d⁡xd⁡φ=d⁡d⁡φr⋅cos⁡φ=r˙cos⁡φ−rsin⁡φ\dot x= \dfrac{\d x}{\d \phi}= \dfrac\d {\d \phi}r\cdot \cos\phi=\dot r\cos\phi-r\sin\phi
und
y˙=d⁡yd⁡φ=d⁡d⁡φr⋅sin⁡φ=r˙sin⁡φ+rcos⁡φ\dot y= \dfrac{\d y}{\d \phi}= \dfrac\d {\d \phi}r\cdot \sin\phi=\dot r\sin\phi+r\cos\phi
 
 

Formel 15W9 (Ableitung in Polarkoordinaten)

y′=r˙sin⁡φ+rcos⁡φr˙cos⁡φ−rsin⁡φy'=\dfrac {\dot r\sin\phi+r\cos\phi}{\dot r\cos\phi-r\sin\phi}(1)

Beispiel

Der Kreis hat in Polarkoordinaten die Darstellung r=r0r=r_0. Die Ableitungen ergeben sich dann mit x˙=−r0sin⁡φ\dot x=-r_0\sin\phi und y˙=r0cos⁡φ\dot y=r_0\cos\phi.
PkWinkel.png
Wollen wir nun den Winkel zwischen Radiusvektor und Tangentenvektor bestimmen, so gilt τ=α−φ\tau=\alpha-\phi.
tan⁡τ=tan⁡(α−φ)\tan\tau=\tan(\alpha-\phi) =sin⁡(α−φ)cos⁡(α−φ)=\dfrac{\sin(\alpha-\phi)}{\cos(\alpha-\phi)}
=sin⁡αcos⁡φ−sin⁡φcos⁡αcos⁡αcos⁡φ+sin⁡αsin⁡φ=\dfrac {\sin\alpha\cos\phi-\sin\phi\cos\alpha}{\cos\alpha\cos\phi+\sin\alpha\sin\phi} (Satz 5220A)
=tan⁡αcos⁡φ−sin⁡φtan⁡αsin⁡φ+cos⁡φ=\dfrac{\tan\alpha\cos\phi-\sin\phi}{\tan\alpha\sin\phi+\cos\phi} (Ausklammern von cos⁡α\cos\alpha)
=y′cos⁡φ−sin⁡φy′sin⁡φ+cos⁡φ=\dfrac{y'\cos\phi-\sin\phi}{y'\sin\phi+\cos\phi} (Nach Definition der Ableitung ist y′=tan⁡αy'=\tan\alpha)
Also:
tan⁡τ=y′cos⁡φ−sin⁡φy′sin⁡φ+cos⁡φ\tan\tau=\dfrac{y'\cos\phi-\sin\phi}{y'\sin\phi+\cos\phi}(2)
Jetzt machen wir eine kleine Zwischenrechnung. Wir stellen (1) nach r˙r\dfrac {\dot r} r um.
y′=r˙sin⁡φ+rcos⁡φr˙cos⁡φ−rsin⁡φ=r˙rsin⁡φ+cos⁡φr˙rcos⁡φ−sin⁡φy'=\dfrac {\dot r\sin\phi+r\cos\phi}{\dot r\cos\phi-r\sin\phi}=\dfrac {\dfrac {\dot r} r \sin\phi+\cos\phi}{\dfrac {\dot r} r \cos\phi-\sin\phi}
  ⟹  y′(r˙rcos⁡φ−sin⁡φ)=r˙rsin⁡φ+cos⁡φ\implies y'\braceNT{\dfrac {\dot r} r \cos\phi-\sin\phi}={\dfrac {\dot r} r \sin\phi+\cos\phi}   ⟹  y′r˙rcos⁡φ−y′sin⁡φ=r˙rsin⁡φ+cos⁡φ\implies y'\dfrac {\dot r} r \cos\phi-y'\sin\phi={\dfrac {\dot r} r \sin\phi+\cos\phi}   ⟹  r˙r(y′cos⁡φ−sin⁡φ)=y′sin⁡φ+cos⁡φ\implies \dfrac {\dot r} r (y'\cos\phi-\sin\phi)=y'\sin\phi+\cos\phi. Also:
r˙r=y′sin⁡φ+cos⁡φy′cos⁡φ−sin⁡φ\dfrac {\dot r} r=\dfrac {y'\sin\phi+\cos\phi}{y'\cos\phi-\sin\phi}.
Vergleichen wir dieses Ergebnis nun mit (2), ergibt sich

Formel 15WA (Winkel von Tangente und Radiusvektor in Polarkoordinaten)

tan⁡τ=rr˙\tan\tau=\dfrac r {\dot r}

Wir Mathematiker sind die wahren Dichter, nur müssen wir das, was unsere Phantasie schafft, noch beweisen.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene Kurven