Beispiele

Spiralen

Archimedische Spirale

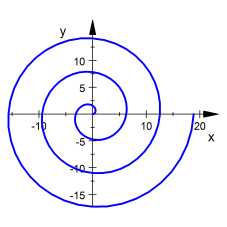
ArchSpiral.png
Die Gleichung in Polarkoordinaten
r(φ)=a⋅φr(\phi)=a\cdot\phi (a∈Ra\in\domR)
definiert eine ebene Kurve, die archimedische Spirale.
Der Abstand eines Punktes zum Ursprung ist dabei proportional zum Winkel φ\phi.
Ausführliche Darstellung: Archimedische Spirale
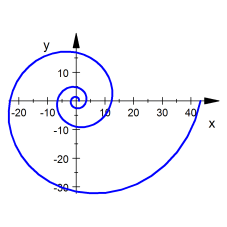
LogSpirale.png

Logarithmische Spirale

Die Gleichung in Polarkoordinaten
r(φ)=e⁡a⋅φr(\phi)=\e^{a\cdot\phi} (a∈Ra\in\domR)
definiert eine ebene Kurve, die logarithmische Spirale.
Der Abstand eines Punktes zum Ursprung wächst dabei exponential mit dem Winkel φ\phi.
 
 

Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.

Karl Weierstraß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Kurventheorie