Archimedische Spirale

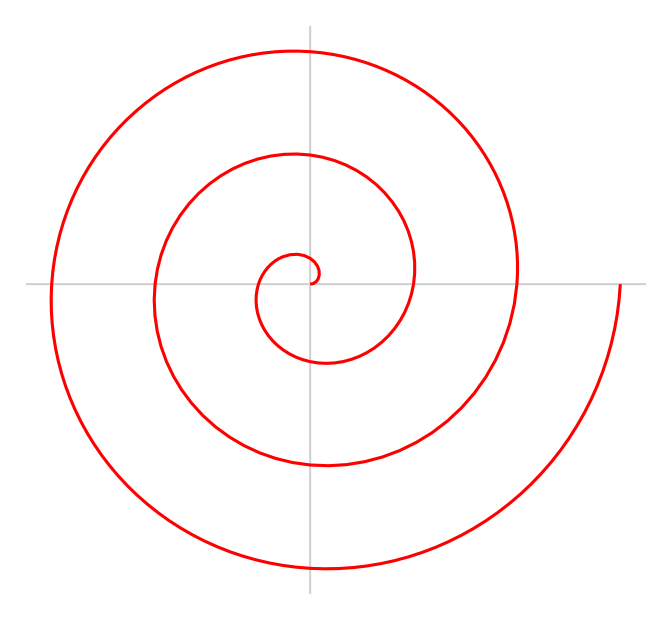
Archimedean_spiral.png
Archimedische Spirale - mit konstantem Windungsabstand
Die Archimedische Spirale entsteht, wenn bei einer Drehbewegung der Radius proportional zum Drehwinkel wächst, das heißt es gilt r=a⋅φ r=a\cdot \varphi mit Radius r r , Drehwinkel φ \varphi und a≥0 a\geq 0 .

Eigenschaften

Eine besondere Eigenschaft der archimedischen Spirale ist ihr konstanter Windungsabstand, der a⋅2⋅π a\cdot 2 \cdot \pi beträgt. Die Darstellung als Parameterkurve in kartesischen Koordinaten lautet:
f:φ↦(r⋅cos⁡φ,r⋅sin⁡ φ)=(a⋅φ⋅cos⁡ φ,a⋅φ⋅sin⁡ φ) f:\varphi \mapsto (r\cdot\cos\varphi, r\cdot\sin\, \varphi ) = (a\cdot \varphi\cdot\cos\,\varphi ,a\cdot \varphi\cdot\sin\,\varphi ) .
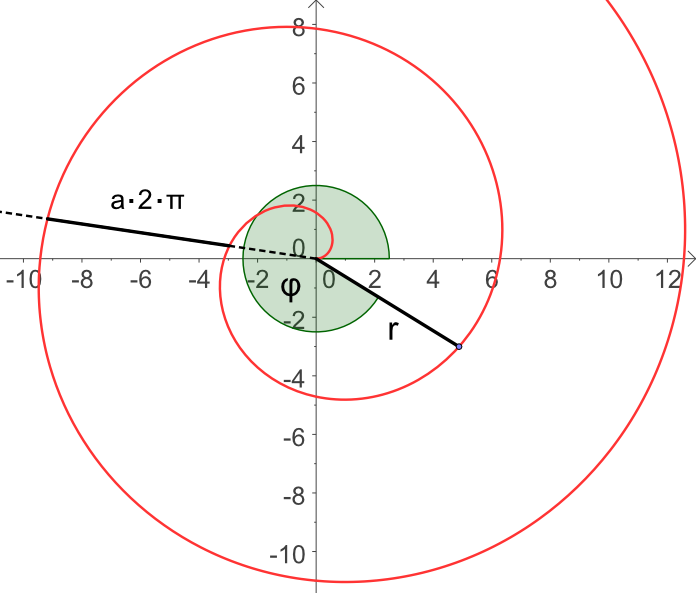
Archimedean_spiral2.png
Archimedische Spirale - mit Parametern

Bogenlänge

Die Länge eines Bogenstücks von φ1\varphi_1 bis φ2 \varphi_2 ist
a2[φ⋅1+φ2+ln⁡(φ+1+φ2)]φ1φ2\dfrac{a}{2}\left[\varphi\cdot\sqrt{1+\varphi^2}+\ln\left(\varphi+\sqrt{1+\varphi^2}\right)\right]_{\varphi_1}^{\varphi_2}
oder kurz: a2[φ⋅1+φ2+arsinh φ]φ1φ2\dfrac{a}{2}\left[\varphi\cdot\sqrt{1+\varphi^2}+\mathrm{arsinh}\,\varphi\right]_{\varphi_1}^{\varphi_2}
Die Gesamtlänge der Spirale von φ1=0\varphi_1=0 bis φ2=φ\varphi_2=\varphi ist folglich
a2[φ⋅1+φ2+ln⁡(φ+1+φ2)] \dfrac{a}{2}\left[\varphi\cdot\sqrt{1+\varphi^2}+\ln \left(\varphi+\sqrt{1+\varphi^2} \right)\right]\,

Fläche

Die Fläche, die bei der ersten Umdrehung eingeschlossen wird, ist
43π3a2,\dfrac{4}{3}\pi^3a^2,
während bei der n-ten Umdrehung die Fläche
8(n−1)π3a28(n-1)\pi^3a^2
zusätzlich eingeschlossen wird.

Historisches

Archimedes beschrieb die nach ihm benannte Spirale 225 v. Chr. in seiner Abhandlung "Über Spiralen", sie war allerdings schon vorher seinem Freund und Zeitgenossen Konon von Samos bekannt, der als ihr Entdecker gilt. Im 4. Jahrhundert n. Chr. wurde sie von Pappos untersucht. Die allgemeine Bestimmung der Spirallänge gelang Isaac Barrow 1670.

Verallgemeinerungen

Es gibt verschiedene Verallgemeinerungen der ursprünglich von Archimedes beschrieben Spirale, für die in der Literatur auch oft archimedische Spiralen als Sammelbegriff verwendet wird. Hierbei wird die ursprüngliche Gleichung r=a⋅φ r=a\cdot \varphi zu r=a⋅φ1d r=a\cdot \varphi^\frac{1}{d} mit d∈Rd\in\mathbb{R} erweitert. Für d=1 d=1 erhält man wieder die gewöhnliche Spirale des Archimedes, d=2 d=2 wird auch als fermatsche Spirale bezeichnet. Generell können sich diese Spiralen in Eigenschaften und Aussehen deutlich von der ursprünglichen archimedischen Spirale unterscheiden und insbesondere besitzen sie keinen konstanten Windungsabstand.
 
 

Es gibt keinen Königsweg zur Mathematik.

Euklid

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Archimedische Spirale aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene Kurven