Umkreisradius und Umfangsradius

Sei $F$ eine konvexe Figur mit dem Umfangsradius $r_u$ und dem Umkreisradius $R$. Dann gilt: Die Gleichheit gilt genau dann, wenn $F$ ein Kreis ist.

Die Behauptung ist äquivalent zur Aussage, dass der Umfang der Figur kleiner als der Umfang des Umkreises ist.

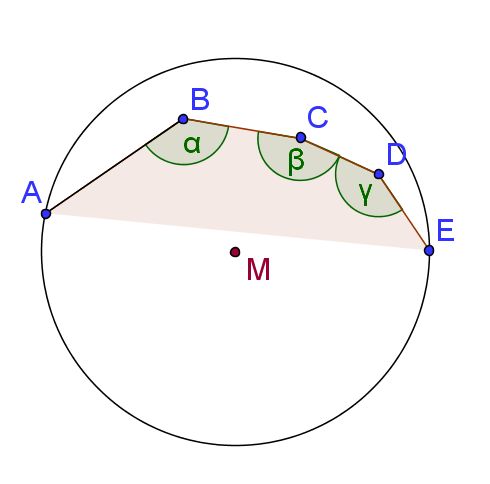
Wir zeigen die Behauptung für Polygone. Der Umkreis eines Polygon existiert nach Satz C8N9 stets. Er berührt das Polygon in einer endlichen Anzahl von Punkten. Wir betrachten die Polygonstücke zwischen diesen Punkten und zeigen, dass diese kürzer als die entsprechen Kreisbögen sind. Wegen der Konvexität des Polygons, sind alle Innenwinkel kleiner als $180°$, also z.B. die Winkel $\alpha$, $\beta$ und $\gamma$ in der [!Abbildung].

Wir unterscheiden zwei wesentliche Fälle: 1) Strecken wie $\ovl{AB}$, die einen Punkt mit dem Umkreis gemeinsam haben und 2) Strecken wie z.B. $\ovl{CD}$, die keinen Punkt mit dem Umkreis gemeinsam haben. (Der Fall, bei dem beide Endpunkte der Strecke auf dem Umkreis liegen ist trivial.)

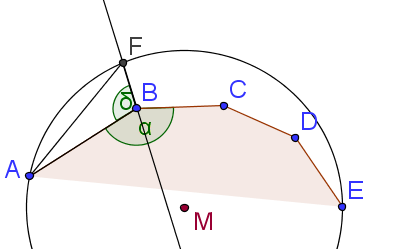
Fall 1: Wir halbieren den Innenwinkel bei $B$. Sei $F$ der Punkt, wo die Winkelhalbierende den Umkreis schneidet. Nun ist $\alpha /2<=90°$ und damit $\delta>=90°$ der größte Winkel im Dreieck $\triangle ABF$ und damit ist $\ovl{AF}$ die längste Seite. Sie ist sicher länger als $\ovl{AB}$, also ist $\ovl{AB}$ kürzer als der Kreisbogen zwischen $A$ und $F$.

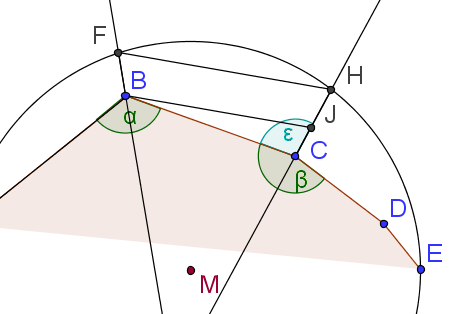
Fall 2: Wir halbieren die Innenwinkel bei $B$ und $C$ und die zugeordneten Winkelhalbierenden schneiden den Umkreis in $F$ und $H$. Wir bilden die Parallele zur Strecke $\ovl{FH}$ durch den Punkt $B$ (bzw. $G$ falls dieser näher an $\ovl{FH}$ liegt, die nachfolgenden Beweisschritte werden dann analog mit dem Winkel $\alpha$ geführt). Da $\beta<=180°$ gilt $\epsilon>=90°$ und wie mit den gleichen Argumenten wie in Schritt 1 erhalten wir $\ovl{BJ}>=\ovl{BC}$ und nach Strahlensatz muss auch $\ovl{FH}>=\ovl{BJ}$ gelten.

Ist die Figur kein Polygon so gehen wir analog zur Definition des bestimmten Integrals vor. Der Weg soll hier nur skizziert werden. Wir definieren für eine beliebige (aber endliche) Menge von Punkten auf dem Rand der Figur ein Polygon, das genau durch die aufeinanderfolgenden Verbindungsstrecken dieser Punkte bestimmt wird. Für jedes dieser Polygone ist die Ungleichung erfüllt. Dann bilden wir das Supremum von Längen aller dieser Polygone. Dieses entspricht dem Umfang der Figur, ist aber kleiner oder gleich dem Umkreisradius.

Sei $F$ eine konvexe Figur für die $r_u=R$ gilt und $K$ der Umkreis. Eine beliebige Gerade $g$ durch den Mittelpunkt des Umkreises teilt $F$ in zwei Teilfiguren mit gleichem Teilumfang. Wäre dies nicht so, könnte man die längere Teilfgur an $g$ spielen und erhielte eine Figur für die $r_u>R$ gilt, im Widerspruch zum 1. Teil des Satzes. Damit ist $F$ spiegelsymmetrisch zu allen Geraden durch den Mittelpunkt des Umkreises, und damit selbst ein Kreis, dessen Mittelpunkt mit dem des Umkreises zusammenfällt. Da beide Kreise den gleichen Umfang haben, sind sie damit identisch. $\qed$

Für allgemeine (nicht konvexe) Figuren muss Satz C93F nicht gelten. Denn wir können den Umfang einer Figur durch Einbuchtungen (oder Zacken) beliebig vergrößern ohne dass sich der Umkreis ändert.