Existenz des minimalen Umkreises für endliche Punktmengen

Der Umkreisradius ist wohldefiniert; dies sagt jedoch nichts über die Existenz eines Umkreises mit genau diesem Radius aus.

Die Existenz des minimalen Umkreises ist jedoch gesichert, falls $\inf K_R=\min K_R$, also $R\in K_R$ gilt. Dann gibt gibt es zu diesem Minimum einen zugeordneten Kreis. Falls $K_R$ endlich ist, stimmt dies trivialerweise.

Sein $S\subset \R^2$ eine endliche Punktmenge. Da die Umkreise von Polygonen mit den Umkreisen ihre Eckpunktmengen übereinstimmen, ist damit auch die Existenz minimaler Umkreise zu Polygonen gesichert.

Sei $\mathcal K$ die Menge aller Umkreise von $M$. Wir konstruieren eine Abbildung $\phi: \mathcal K\to\mathcal K$, die jedem Umkreis einen Umkreis mit einem nicht größeren Radius zuordnet und so, dass die Bildmenge $\phi (\mathcal K)$ endlich ist. Ordne nun $r:\mathcal K\to\R$ jedem Umkreis seinen Radius zu. Dann gilt: $r(\phi(k))<=r(K)$ für alle $K\in\mathcal K$ und da wir für einen beliebigen Umkreis $K$ immer einen Umkreis aus $\phi(\mathcal K)$ finden können, dessen Radius nicht größer ist - nämlich $\phi(K)$ - gilt sogar $\inf_{K\in\mathcal K} r(\phi(k))=\inf_{K\in\mathcal K} r(k)$ und mit der Endlichkeit von $\phi (\mathcal K)$, wäre die Existenz gezeigt.

Bleibt die Konstruktion von $\phi$. Sei $K$ ein beliebiger Umkreis mit dem Mittelpunkt $M$. Wir unterscheiden 3 Fälle.

Fall 1: Der Umfang (Rand) von $K$ enthält keinen Punkt aus $S$. Wir verkleinern den Radius von $K$ solange, bis wenigstens ein Punkt auf dem Umfang von $K$ liegt. Weiter mit Fall 2 , oder 4.

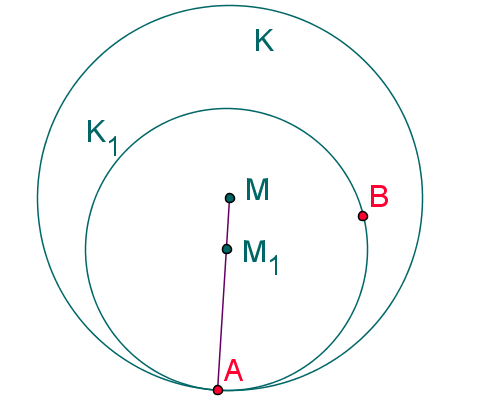
Fall 2: Der Rand von $K$ enthält genau einen Punkt $A$ aus $S$. Wir verschieben den Mittelpunkt $M_1$ eines neuen Umkreises entlang der Strecke $\ovl {AM}$ bis der so entstandene Kreis $K_1$ wenigstens einen weiteren Punkt $B\in S$ berührt.

Weiter mit Fall 3 oder Fall 4. Fall 3: Der Rand von $K$ enthält genau 2 Punkte aus $S$ und seien diese $A$ und $B$. Fall 3.1: $M_K$ liegt auf der Strecke $\ovl{AB}$, dann setzen wir $\phi(K)=K$.

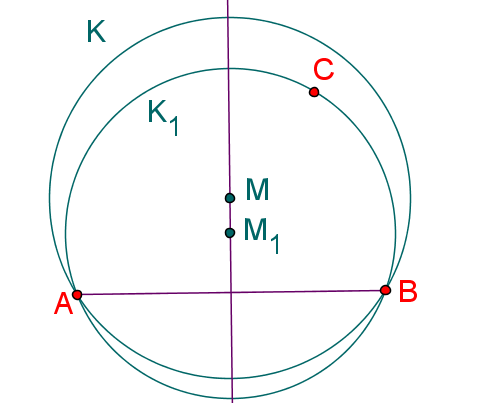
Fall 3.2: $M_K$ liegt nicht auf der Strecke $\ovl{AB}$. Wir verschieben den Mittelpunkt $M_1$ entlang der Mittelsenkrechte in Richtung $\ovl {AB}$. Berührt der so entstanden Kreis einen weiteren Punkt, bevor $M_1$ die Strecke $\ovl{AB}$ erreicht, so haben wir Fall 4. Erreicht $M_1$ jedoch die Strecke $\ovl{AB}$ zuerst, handelt es sich um Fall 3.2. Dann gehen wir wie unter diesen Fällen beschrieben vor.

Fall 4: Der Rand $K$ enthält wenigstens 3 Punkte aus $S$, dann ist $\phi(K)=K$.

Diese Konstruktion ist wohldefiniert und deterministisch, sie liefert für jeden Umkreis einen Umkreis mit kleinerem Radius, der durch eine Teilmenge der Punkte aus $M$ bestimmt wird. Damit kann es nur endlich viele Bilder für alle möglichen Umkreise geben und wir können die obige Argumentation anwenden. $\qed$