Kubische Gleichung

Die allgemeine Gleichung dritten Grades
ax3+bx2+cx+d=0ax^3+bx^2+cx+d=0
mit reellen Zahlen a,b,c,da,b,c,d und a≠0a\ne0 kann durch Division mit aa und Substitution mit y=x+b3ay=x+\dfrac b{3a} in die Form
y3+py+q=0y^3+py+q=0
gebracht werden, wobei
p=3ac−b23a2p=\dfrac {3ac-b^2}{3a^2}
und
q=2b327a3−bc3a2+daq=\dfrac {2b^3}{27a^3} - \dfrac {bc}{3a^2} + \dfrac {d}{a}
gilt.
Es sei D=4p3+27q2D=4p^3+27q^2 die Diskriminante der linken Seite.
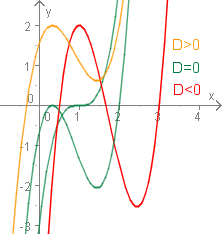
KubDiskr.png
Das Lösungsverhalten hängt nun entscheidend vom Vorzeichen der Diskriminante ab:
  • D>0D>0: Es gibt genau eine reelle Lösung und zwei echt komplexe Lösungen.
  • D=0D=0: Es gibt entweder eine doppelte reelle Lösung und eine einfache reelle Lösung oder eine dreifache reelle Lösung.
  • D<0D<0: Es gibt drei verschiedene reelle Lösungen.
 
 

DD > 0

Es gibt genau eine reelle Lösung, die durch
y1=−q2+(q2)2+(p3)33+−q2−(q2)2+(p3)33y_1=\sqrtN{3}{-\dfrac q2+\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}+\sqrtN{3}{-\dfrac q2-\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}
gegeben ist. (Ist dabei eine dritte Wurzel aus einer negativen Zahl zu ziehen, so ist die negative und nicht eine der beiden echt komplexen Wurzeln zu wählen, d.h. −x3=−x3\sqrtN{3}{-x}=-\sqrtN{3}{x}.)
Die anderen beiden, echt komplexen Lösungen sind im Fall q≠0q\ne0 die Lösungen der quadratischen Gleichung
y2+y1y−qy1=0;y^2+y_1y-\dfrac q{y_1}=0;
im Spezialfall q=0q=0 sind die anderen beiden Lösungen
y2/3=±ip y_{2/3}=\pm\mathrm i\sqrt p\,
Alternativ kann man die komplexen Lösungen auch direkt angeben: Es sei
ω=−1+i32\omega=\dfrac{-1+\mathrm i\sqrt3}2
eine dritte Einheitswurzel. Dann sind die Lösungen:
y2=ω−q2+(q2)2+(p3)33+ωˉ−q2−(q2)2+(p3)33y_2=\omega\sqrtN{3}{-\dfrac q2+\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}+\bar\omega\sqrtN{3}{-\dfrac q2-\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}
y3=ωˉ−q2+(q2)2+(p3)33+ω−q2−(q2)2+(p3)33y_3=\bar\omega\sqrtN{3}{-\dfrac q2+\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}+\omega\sqrtN{3}{-\dfrac q2-\sqrt{\braceNT{\dfrac q2}^2+\braceNT{\dfrac p3}^3}}

DD = 0

In diesem Fall gibt es eine doppelte reelle Lösung
y1/2=−3q2p=q23y_{1/2}=-\dfrac{3q}{2p}=\sqrtN{3}{\dfrac q2}
und eine einfache Lösung
y3=3qp=−4q3 y_3=\dfrac{3q}p=\sqrtN{3}{-4q}\,
Ist p=q=0p=q=0, so ist y=0y=0 die einzige (dreifache) Lösung.

DD < 0 (casus irreducibilis)

Es gibt drei verschiedene reelle Lösungen, bei ihrer Bestimmung mit der obigen Formel müssen jedoch dritten Wurzeln aus echt komplexen Zahlen berechnet werden. Deshalb wird dieser Fall casus irreducibilis genannt.
Mithilfe der trigonometrischen Funktionen können die Wurzeln jedoch berechnet werden:
y1=2 −p3⋅cos⁡(13arccos⁡(−q2⋅−27p3))y_1 = 2\, \sqrt{-\dfrac{p}{3}}\cdot \cos\braceNT{\dfrac{1}{3}\arccos\braceNT{\dfrac{-q}{2}\cdot\sqrt{-\dfrac{27}{p^3}}}}
y2=−2 −p3⋅cos⁡(13arccos⁡(−q2⋅−27p3)+π3)y_2 = -2\, \sqrt{-\dfrac{p}{3}}\cdot \cos\braceNT{\dfrac{1}{3}\arccos\braceNT{\dfrac{-q}{2}\cdot\sqrt{-\dfrac{27}{p^3}}} + \dfrac{\pi}{3}}
y3=−2 −p3⋅cos⁡(13arccos⁡(−q2⋅−27p3)−π3)y_3 = -2\, \sqrt{-\dfrac{p}{3}}\cdot \cos\braceNT{\dfrac{1}{3}\arccos\braceNT{\dfrac{-q}{2}\cdot\sqrt{-\dfrac{27}{p^3}}} - \dfrac{\pi}{3}}

Cardanische Formeln

Die obigen Formeln tragen den Namen Cardanischen Formeln. Sie wurden, zusammen mit Lösungsformeln für biquadratische Gleichungen (Gleichungen 4. Grades), erstmals 1545 von dem Mathematiker Gerolamo Cardano in seinem Buch Ars magna veröffentlicht. Entdeckt wurde die Lösungsformel für kubische Gleichungen von Tartaglia; laut Cardano sogar noch früher durch Scipione del Ferro.
Die Cardanischen Formeln waren eine wichtige Motivation für die Einführung der komplexen Zahlen, da man im Fall des casus irreducibilis durch das Ziehen einer Quadratwurzel aus einer negativen Zahl zu reellen Lösungen gelangen kann.
Die Cardanischen Formeln besitzen bei der numerischen Lösung von Gleichungen heute keine praktische Bedeutung mehr. Der Nachweis, dass es keine entsprechenden Formeln für Gleichungen fünften und höhreren Grades geben kann, hat allerdings die Entwicklung der Algebra entscheidend befruchtet (siehe Galoistheorie).

Komplexe Koeffizienten

Das Vorgehen ist für komplexe Koeffizienten weitgehend analog, es gibt aber nur zwei Fälle:
  • D≠0D\ne0: Die oben für den Fall D>0D>0 angegebenen Formeln gelten analog; die beiden dritten Wurzeln sind dabei so zu wählen, dass ihr Produkt −p/3-p/3 ergibt.
  • D=0D=0: Die oben für den Fall D=0D=0 angegebenen Formeln gelten unverändert.

Literatur

  • Jörg Bewersdorff: Algebra für Einsteiger: Von der Gleichungsauflösung zur Galois-Theorie, Wiesbaden 2004, ISBN 3528131926
  • Heinrich Dörrie: Kubische und biquadratische Gleichungen, München 1948
  • Ludwig Matthiessen: Grundzüge der antiken und modernen Algebra der litteralen Gleichungen, Leipzig 1896

Die Furcht vor der Mathematik steht der Angst erheblich näher als der Ehrfurcht.

Felix Auerbach

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Cardanische Formeln aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Algebra