Homomorphiesatz

Bisher haben wir die Normalteiler als Kerne von Gruppenhomomorphismen charakterisiert. Jetzt können wir dieses Ergebnis erweitern:

Satz 5213F (Homomorphiesatz)

Seien GG und HH zwei Gruppen und f:G→Hf:G\rightarrow H ein Homomorphismus, ker(f)\Ker(f) der Kern von ff und im(f)\Image(f) das Bild von ff. Dann ist die Faktorgruppe G/ker(f)G/\Ker(f) isomorph zu im(f)\Image(f):
G/ker(f)≅im(f)G/\Ker(f)\cong\Image(f)
 
 

Beweis

Zuerst wollen wir und den zu beweisenden Sachverhalt weiter klar machen. Wir setzen abkürzend N:=ker(f)N:=\Ker(f) und h:G→Nh: G\rightarrow N den kanonischen Homomorphismus (h(g)=gNh(g)=gN).
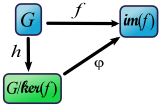
homo.png
Als gesuchter Isomorphismus φ:N→im(f)\phi: N\rightarrow \Image(f) wird sich gerade folgende Abbildung herausstellen: φ(gN):=f(g)\phi(gN):=f(g). Der Nebenklasse gNgN wird also das Bild von gg unter ff zugeordnet.
Nebenstehende Skizze verdeutlicht die einzelnen Abbildungen.
Wir haben folgende Äquivalenzkette:
aN=bN  ⟺  a−1b∈NaN=bN\iff a^{-1}b\in N (Lemma 5211A)
  ⟺  f(a−1b)=1H\iff f(a^{-1}b)=1_H (Definition von ker(f)\Ker (f))
  ⟺  f(a)−1f(b)=1H\iff f(a)^{-1}f(b)=1_H (Satz 5213B und ff ist Homomorphismus)
  ⟺  f(a)=f(b)  ⟺  φ(aN)=φ(bN)\iff f(a)=f(b)\iff \phi(aN)=\phi(bN) (Definition von φ\phi)
Damit haben wir nicht nur gezeigt, dass φ\phi wohldefiniert ist, sondern auch die Injektivität.
Die Surjektivität von φ\phi ergibt sich sofort aus der Definition.
Jetzt müssen wir nur noch zeigen, dass φ\phi auch ein Homomorphismus ist.
Es gilt φ(aNbN)=φ(abN)\phi(aNbN)= \phi(abN) (NN ist nach Satz 5213C Normalteiler)
=f(ab)=f(a)f(b)=f(ab)=f(a)f(b) =φ(aN)φ(bN)=\phi(aN)\phi(bN). □\qed

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gruppen