Bestimmtes Integral und Stammfunktion
Satz 15VL (Bestimmtes Integral und Stammfunktion)
∫ a b f ( x ) d x = F ( b ) − F ( a ) \int\limits_a^b f(x)\; dx= F(b)-F(a) a ∫ b f ( x ) d x = F ( b ) − F ( a ) Das
bestimmte Integral entspricht also der
Differenz der Werte der
Stammfunktion an den Integrationsgrenzen. Weitere Schreibweisen:
F ( x ) ∣ a b F(x)\big|_a^b F ( x ) ∣ ∣ a b und
[ F ( x ) ] a b \left[F(x)\right]_a^b [ F ( x ) ] a b Beweis
Sei
Z = { x 0 , … , x n } Z=\{x_0,\ldots,x_n\} Z = { x 0 , … , x n } eine beliebige
Zerlegung von
[ a , b ] [a,b] [ a , b ] . Nach dem
Mittelwertsatz der Differentialrechnung gibt es ein
ξ j ∈ ] x j − 1 , x j [ \xi_j\in ]x_{j-1},x_j[ ξ j ∈ ] x j − 1 , x j [ , sodass
F ( x j ) − F ( x j − 1 ) = F ′ ( ξ j ) ⎵ = f ( ξ j ) ⋅ ( x j − x j − 1 ) F(x_j)-F(x_{j-1}) \; {=}\; \underbrace{F\, '(\xi_j)}_{=f(\xi_j)}\cdot (x_j-x_{j-1}) F ( x j ) − F ( x j − 1 ) = = f ( ξ j ) F ′ ( ξ j ) ⋅ ( x j − x j − 1 ) wobei
f ( ξ j ) > = m j f(\xi_j)>=m_j f ( ξ j ) > = m j und
f ( ξ j ) < = M j f(\xi_j)<=M_j f ( ξ j ) < = M j gilt mit
I j : = [ x j − 1 , x j ] I_j:=[x_{j-1}, x_j] I j : = [ x j − 1 , x j ] ,
m j : = inf f ( I j ) m_j:=\inf f(I_j) m j : = inf f ( I j ) und
M j : = sup f ( I j ) M_j:=\sup f(I_j) M j : = sup f ( I j ) .
⇒ m j ∣ I j ∣ ≤ F ( x j ) − F ( x j − 1 ) ≤ M j ∣ I j ∣ \Rightarrow\; m_j|I_j|\leq F(x_j)-F(x_{j-1})\leq M_j|I_j| ⇒ m j ∣ I j ∣ ≤ F ( x j ) − F ( x j − 1 ) ≤ M j ∣ I j ∣ ⇒ s f ( Z ) ≤ ∑ j = 1 n ( F ( x j ) − F ( x j − 1 ) ) ⎵ F ( x n ) − F ( x n − 1 ) + F ( x n − 1 ) − F ( x n − 2 ) + ⋯ ≤ S f ( Z ) \Rightarrow\; s_f(Z)\;\leq \underbrace{\sum\limits_{j=1}^n (F(x_j)-F(x_{j-1}))}_{\atop{F(x_n)-F(x_{n-1})}{+F(x_{n-1})-F(x_{n-2})+\cdots}}\;\leq S_f(Z) ⇒ s f ( Z ) ≤ F ( x n ) − F ( x n − 1 ) + F ( x n − 1 ) − F ( x n − 2 ) + ⋯ j = 1 ∑ n ( F ( x j ) − F ( x j − 1 ) ) ≤ S f ( Z ) ⇒ s f ≤ F ( b ) − F ( a ) ≤ S f = s f \Rightarrow\; s_f\;\leq\; F(b)-F(a)\;\leq\; S_f=s_f ⇒ s f ≤ F ( b ) − F ( a ) ≤ S f = s f wegen
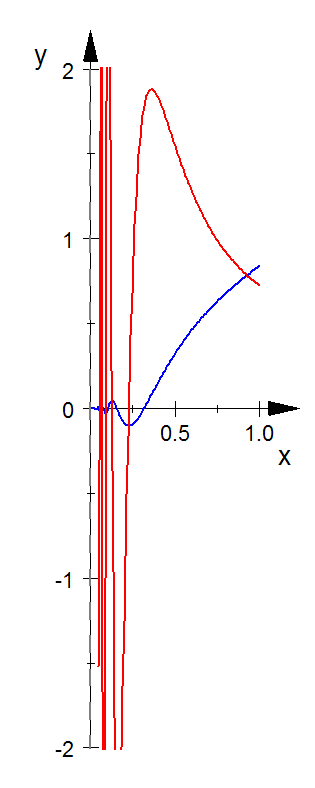
f ∈ R [ a , b ] f\in R[a,b] f ∈ R [ a , b ] ⇒ F ( b ) − F ( a ) = S f = s f \Rightarrow\; F(b)-F(a)=S_f=s_f ⇒ F ( b ) − F ( a ) = S f = s f = ∫ a b f ( x ) d x =\int\limits_a^b f(x)\; dx = a ∫ b f ( x ) d x □ \qed □ F ( x ) F(x) F ( x ) blau und
f ( x ) = F ′ ( x ) f(x)=F\, '(x) f ( x ) = F ′ ( x ) rot
Beispiele
Beispiel
Es gibt
Funktionen , die
Stammfunktionen besitzen, aber nicht
integrierbar sind.
F ( x ) = { x 3 2 sin 1 x f u ¨ r x ∈ ] 0 , 1 ] 0 f u ¨ r x = 0 F(x)=\begin{cases} x^\dfrac{3}{2}\sin\dfrac{1}{x}& \text{ für }x\in ]0,1]\\0 & \text{für }x=0\end{cases} F ( x ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 2 3 sin x 1 0 f u ¨ r x ∈ ] 0 , 1 ] f u ¨ r x = 0 F F F ist
differenzierbar auf
[ 0 , 1 ] [0,1] [ 0 , 1 ] . Die
Funktion f : = F ′ = 3 2 x ⋅ sin 1 x − 1 x ⋅ cos 1 x f:=F'=\dfrac 3 2{\sqrt x}\cdot\sin\dfrac 1 x - \dfrac 1{\sqrt x}\cdot\cos\dfrac 1x f : = F ′ = 2 3 x ⋅ sin x 1 − x 1 ⋅ cos x 1 ist auf
[ 0 , 1 ] [0,1] [ 0 , 1 ] unbeschränkt und daher nicht
integrierbar . Jedoch hat
f f f eine
Stammfunktion , nämlich
F F F .
Beispiel
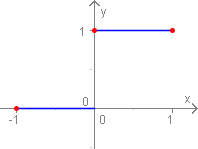
f ( x ) : = { 0 f u ¨ r x ∈ [ − 1 , 0 [ 1 f u ¨ r x ∈ [ 0 , 1 ] f(x):=\begin{cases} 0& \text{ für }x\in [-1,0[\\ 1& \text{für }x\in [0,1]\end{cases} f ( x ) : = { 0 1 f u ¨ r x ∈ [ − 1 , 0 [ f u ¨ r x ∈ [ 0 , 1 ] f f f ist
monoton und ist daher nach
Satz 16MG integrierbar auf
[ − 1 , 1 ] [-1,1] [ − 1 , 1 ] . Angenommen es existiert eine
Stammfunktion F F F zu
f f f auf
[ − 1 , 1 ] [-1,1] [ − 1 , 1 ] .
⇒ F ´ = 0 \Rightarrow\; F´=0 ⇒ F ´ = 0 auf
[ − 1 , 0 [ [-1,0[ [ − 1 , 0 [ ⇒ F ≡ c 1 \;\Rightarrow\; F\equiv c_1 ⇒ F ≡ c 1 (
Folgerung 16MC ) auf
[ − 1 , 0 [ [-1,0[ [ − 1 , 0 [ bzw.
F ´ ≡ 1 F´\equiv 1 F ´ ≡ 1 auf
[ 0 , 1 ] [0,1] [ 0 , 1 ] ⇒ F ( x ) = x + c 2 \;\Rightarrow\; F(x)=x+c_2 ⇒ F ( x ) = x + c 2 auf
[ 0 , 1 ] [0,1] [ 0 , 1 ] . Wäre
F F F differenzierbar , so wäre
F F F stetig in
0 0 0 .
⇒ c 1 = c 2 \Rightarrow c_1=c_2 ⇒ c 1 = c 2 und
0 = lim x → 0 − F ( x ) − F ( 0 ) x − 0 = lim x → 0 + F ( x ) − F ( 0 ) x − 0 = F ′ ( 0 ) = f ( 0 ) = 1 0={\lim_{x\to 0-} \dfrac{F(x)-F(0)}{x-0}}=\lim_{x\to 0+} \dfrac{F(x)-F(0)}{x-0}=F\, '(0)=f(0)=1 0 = lim x → 0 − x − 0 F ( x ) − F ( 0 ) = lim x → 0 + x − 0 F ( x ) − F ( 0 ) = F ′ ( 0 ) = f ( 0 ) = 1 . Widerspruch.
Beispiel
∫ a b 1 x d x = ln b − ln a = ln ( b a ) \int\limits_a^b\dfrac{1}{x}\, dx =\ln b-\ln a=\ln\left(\dfrac{b}{a}\right) a ∫ b x 1 d x = ln b − ln a = ln ( a b ) Beispiel
f ( x ) = cos x f(x)=\cos x f ( x ) = cos x ist auf
[ 0 , π 2 ] \left[0, \dfrac{\pi}{2}\right] [ 0 , 2 π ] riemannintegrierbar , da
f f f dort
monoton ist.
F ( x ) : = sin x F(x):=\sin x F ( x ) : = sin x ist
Stammfunktion und
differenzierbar auf
[ 0 , π 2 ] \left[0, \dfrac{\pi}{2}\right] [ 0 , 2 π ] mit
F ′ = f F'=f F ′ = f . Also gilt:
∫ 0 π 2 cos x d x \int\limits_0^\dfrac{\pi}{2} \cos x \, dx 0 ∫ 2 π cos x d x = sin ( π 2 ) − sin ( 0 ) = 1 = \sin\left(\dfrac{\pi}{2}\right)-\sin(0)=1 = sin ( 2 π ) − sin ( 0 ) = 1 Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.
Albert Einstein
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе