Hermitesches Polynome
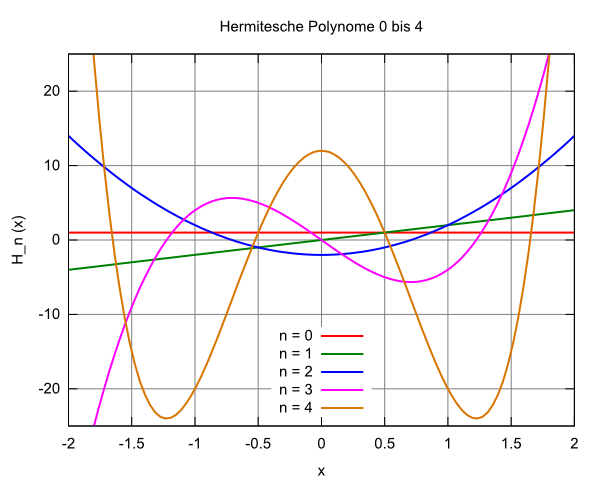
Die Hermiteschen Polynome sind Polynome mit folgenden äquivalenten Darstellungen:
bzw.
Die ersten Polynome lauten explizit
Rekusrionsformeln
Hermitesche Polynome lassen sich durch folgende Rekursionsformeln berechnen:
Da bei jedem Itterationsschritt ein hinzumultipliziert wird, sieht man, dass ein Polynom von Grade ist. Der Koeffizient der höchsten Potenz ist . Für gerade treten ausschließlich gerade Potenzen von auf, entsprechend für ungerade nur ungerade Potenzen, was sich mathematisch durch die Identität
ausdrücken lässt.
Die Hermiteschen Polynome sind die partikulären Lösungen, d.h. jeweils zu einem festen , der linearen Differentialgleichung zweiter Ordnung:
Orthogonalität
Die Hermiteschen Polynome erfüllen bezüglich der Gewichtsfunktion die Orthogonalitätsrelation
Das heißt, dass bestimmte reelle Funktionen nach den Hermiteschen Polynomen in eine Reihe entwickelt werden können.
Ihre Bedeutung erhalten sie durch ihre vielseitige Anwendbarkeit in der Physik. Zum Beispiel werden sie zur Konstruktion der orthonormierten Lösungsfunktionen des quantenmechanischen harmonischen Oszillators benötigt. Diese entsprechen den Hermiteschen Funktionen, die man durch Multiplikation mit der Gaußschen Normalverteilung und geeigneter Normierung erhält.
Andere Darstellung der Hermiteschen Polynome
Eine andere Definitionsmöglichkeit der Hermiteschen Polynome ist
Sie sind bezüglich der Gewichtsfunktion orthogonal
und erfüllen die Differentialgleichung
Sie lassen sich rekursiv durch
bestimmen.
Die Logik ist die Hygiene, deren sich der Mathematiker bedient, um seine Gedanken gesund und kräftig zu erhalten.
Hermann Weyl
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Hermitesches Polynom
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе