Der harmonische Oszillator

In der Physik kann ein schwingendes System oft durch eine lineare Differentialgleichung zweiter Ordnung beschrieben werden. Diese DGL hat die Form
x¨(t)+γx˙(t)+ω02x(t)=F(t)\ddot x(t)+\gamma \dot x(t)+\omega_0^2x(t)=F(t),
wobei xx die schwingende Größe darstellt, die in der Regel von der Zeit tt abhängt.
Der Parameter ω0\omega_0 beschreibt die Eigenfrequenz des Systems und γ\gamma die Reibung, die zu einer Dämpfung der Schwingung führt.
Ist eine treibende Kraft FF vorhanden, so spricht man von einer erzwungenen Schwingung, andernfalls von einer freien Schwingung.

Allgemeine Lösung der homogenen Gleichung/ Ungedämpfte Schwingung

Die homogene Gleichung x¨(t)+γx˙(t)+ω02x(t)=0\ddot x(t)+\gamma \dot x(t)+\omega_0^2x(t)=0 beschreibt eine freie Schwingung und wird mittels eines e⁡\e-Ansatzes gelöst. Wir erhalten dann als charakteristische Gleichung die quadratische Gleichung λ2+γλ+ω02=0\lambda^2+\gamma\lambda+\omega_0^2=0. Ihre allgemeine Lösung ist
λ1,2=−γ2±γ24−ω02\lambda_{1,2}=-\dfrac \gamma 2\pm\sqrt{\dfrac{\gamma^2}4 -\omega_0^2}(1)
und demnach ist die allgemeine Lösung der homogenen Gleichung x(t)=C1e⁡λ1t+C2e⁡λ2tx(t)=C_1\e^{\lambda_1t}+C_2\e^{\lambda_2t}.

Ungedämpfte freie Schwingung

In diesem Fall soll F=0F=0 und γ=0\gamma=0 gelten. Die DGL vereinfacht sich zu x¨(t)+ω02x(t)=0\ddot x(t)+\omega_0^2x(t)=0 und die charakteristische Gleichung hat nur die komplexen Lösungen λ1,2=±−ω02=±i⁡ω\lambda_{1,2}=\pm\sqrt{ -\omega_0^2}=\pm\i\omega. Die allgemeine Lösung ist
y=C1sin⁡ω0t+C2cos⁡ω0ty=C_1\sin\omega_0 t+C_2\cos\omega_0 t
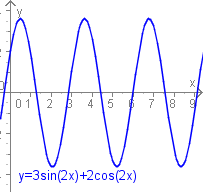
HO1.png
Ungedämpfte freie Schwingung
Bei der Diskussion der allgemeinen Sinusfunktion hatten wir gezeigt, dass hierzu gleichwertig auch eine Sinusfunktion der Form
x(t)=Asin⁡(ω0t+c)x(t)=A\sin(\omega_0t+c)
ist. Es handelt sich um eine kontinuierliche Schwingung mit gleich bleibender Amplitude.

Gedämpfte freie Schwingung

Es soll F=0F=0 und γ>0\gamma> 0 gelten (γ\gamma wird als positiv angenommen, da andernfalls statt einer Dämpfung eine Verstärkung der Schwingung stattfinden würde. Bei Bedarf kann dieser Fall analog diskutiert werden.)
Je nachdem ob die Wurzel in (1) positiv oder negativ wird, sind weitere Fälle zu unterscheiden:
  • Schwache Dämpfung für γ<2ω0\gamma<2\omega_0
  • Starke Dämpfung für γ>2ω0\gamma>2\omega_0
  • Aperiodischer Grenzfall für γ=2ω0\gamma=2\omega_0

Schwache Dämpfung

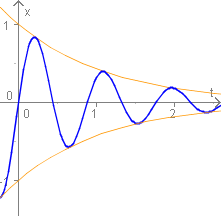
HO2.png
Gedämpfte freie Schwingung mit schwacher Dämpfung
Für γ<2ω0\gamma<2\omega_0 ergibt (1) zwei konjugiert komplexe Lösungen und die homogene DGL hat Lösungen der Form
x(t)=e⁡−γ2t(C1sin⁡ωt+C2cos⁡ωt)x(t)=\e^{-\dfrac \gamma 2 t}(C_1\sin\omega t+C_2\cos\omega t)
mit der verkleinerten Schwingungsfrequenz ω=ω02−γ24\omega=\sqrt{\omega_0^2-\dfrac{\gamma^2}4 }. Die Amplitude der Schwingung nimmt mit der Exponentialfunktion x(t)=e⁡−γ2tx(t)=\e^{-\dfrac \gamma 2 t} ab. Das typische periodische Bild einer Schwingung ist jedoch noch erkennbar, allerdings strebt die Amplitude für t→∞t\to\infty gegen 00.

Starke Dämpfung

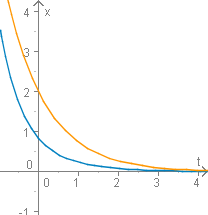
HO3.png
Gedämpfte freie Schwingung mit starker Dämpfung
Für γ>2ω0\gamma>2\omega_0 ergibt (1) lediglich zwei reelle Werte. Die homogene DGL hat Lösungen der Form
x(t)=C1e⁡−δ1t+C2e⁡−δ2tx(t)=C_1\e^{-\delta_1t}+C_2\e^{-\delta_2t}
mit δ1,2=γ2∓γ24−ω02\delta_{1,2}=\dfrac \gamma 2\mp\sqrt{\dfrac{\gamma^2}4 -\omega_0^2}. Zu beachten ist noch, dass beide Wurzeln stets positiv sind, sich also monoton fallende Exponentialfunktionen ergeben. Wegen der starken Dämpfung ist die Periodizität der Schwingung nicht mehr erkennbar.

Aperiodischer Grenzfall

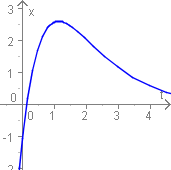
HO4.png
Für γ=2ω0\gamma=2\omega_0 ergibt (1) nur eine Lösung λ=−γ2\lambda=-\dfrac \gamma 2. Die allgemeine Lösung der DGL hat die Form
x(t)=(C1t+C2)e⁡−γ2tx(t)=(C_1t+C_2)\e^{-\frac \gamma 2 t}
Wenn das System wie bei starker Dämpfung nicht sofort ausschwingt, so erreicht es nur ein Extremum, um danach schnell auszuklingen.
 
 

Eine mathematische Wahrheit ist an sich weder einfach noch kompliziert, sie ist.

Émile Lemoine

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Lineare Differentialgleichungen